1) Cas d'une famille de surfaces à un paramètre.
 

Si  est définie par l'équation cartésienne (1) : f(x, y, z, t) = 0, l'équation de l'enveloppe s'obtient en éliminant t entre (1) et l'équation (2) : . Si  est définie paramétriquement par (M(u,v,t))u,v , la résolution de  donne, par élimination d'un des paramètres u,v,t, la paramétrisation de l'enveloppe. Si  est un plan, passant par  et de vecteur normal , l'enveloppe est la surface réglée réunion des droites passant par  et dirigées par .

L'enveloppe d'une famille de surfaces à un paramètre  est la surface  réunion des courbes caractéristiques des surfaces , courbes limites quand  tend vers t des courbes intersections de  avec  ; la surface  est tangente en chacun de ses points à une surface  et "en général", toute surface  est tangente suivant une courbe à  ; les cas restrictifs sont les suivants :
    - sur un intervalle, les surfaces  passent par une courbe fixe, auquel cas, cette courbe appartient à l’enveloppe.
    - les surfaces n'ont pas d'intersection entre elles (par exemple des sphères concentriques, ou des surfaces dont les points d'intersection sont imaginaires).

La famille des courbes caractéristiques  possède alors en général une enveloppe, qui est l'arête de rebroussement de la surface.
Avec les notations ci-dessus dans le cas paramétrique, la condition  étant symétrique en u,v et t, les deux enveloppes des surfaces lieux des points (M(u,v,t))_u,t et des surfaces  lieux des points (M(u,v,t))_v,t sont les mêmes que celle des surfaces  ; l'enveloppe commune est en fait le lieu des points où les surfaces des trois familles sont tangentes suivant une courbe.

Lorsque les surfaces  sont des plans, la courbe caractéristique est une droite qui reste tangente à l'arête de rebroussement de l'enveloppe  (qui est alors une surface réglée développable).

Exemples :
    - la surface polaire d'une courbe est l'enveloppe de ses plans normaux.
    - les cyclides de Dupin et les tubes sont des enveloppes de sphères.
 

2) Cas d'une famille de surfaces à deux paramètres.
 

Si 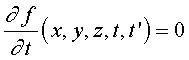 est définie par l'équation cartésienne (1) : f(x, y, z, t, t') = 0, l'équation de l'enveloppe s'obtient en éliminant t et t' entre (1) , (2) :  et (3) : . Si  est définie paramétriquement par (M(u,v,t, t'))u,v , la résolution de ??? (condition pour que ces 4 vecteurs soient coplanaires) donne, par élimination de deux des paramètres u,v,t,t' la paramétrisation de l'enveloppe.

L'enveloppe d'une famille de surfaces à deux paramètres  est la surface  engendrée par les points caractéristiques  des surfaces , points limites quand (t₁ ,t'₁) tend vers (t ,t') des  intersections de  avec  ??? ; la surface  est tangente en chacun de ses points à une surface  et "en général", toute surface  est tangente en au moins un point à .

Avec les notations ci-dessus dans le cas paramétrique, la condition  étant symétrique en u,v,t,t' , l'enveloppe des  est aussi l'enveloppe de 3 autres familles à deux paramètres ; l'enveloppe commune est en fait le lieu des points où les surfaces des 4 familles sont tangentes.

Exemples :
 - Toute surface est l'enveloppe de ses plans tangents.
 - Les surfaces parallèles à une surface sont les enveloppes de sphères de rayon constant centrés sur cette surface.
 - La podaire d'une surface  par rapport à un point O est l'enveloppe des sphères de diamètre [OM] où M décrit .
 - La polaire (réciproque) d'une surface  par rapport à une sphère (S) est l'enveloppe des plans polaires par rapport à (S) des points de .
 - L'enveloppe du plan d'un triangle [ABC] dont les extrémités se déplacent sur les axes Ox, Oy et Oz est
        - une surface astroïdale :  quand la distance du centre de gravité à O est constante
        - la surface cubique : xyz = a³ quand le tétraèdre OABC a un volume constant
 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2016