Paramétrisation cartésienne : .

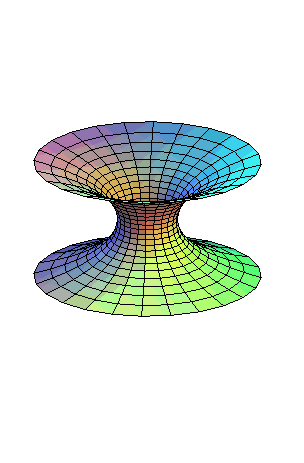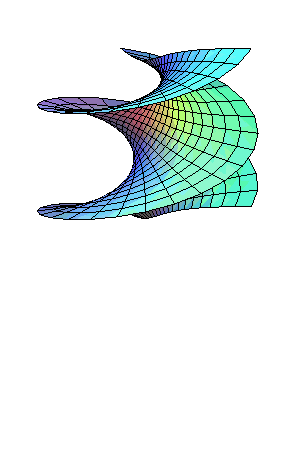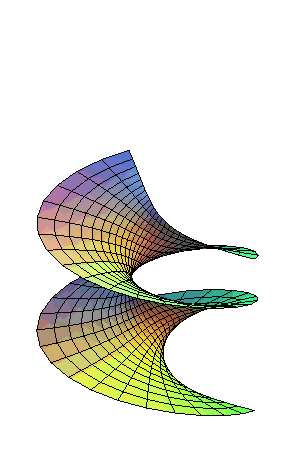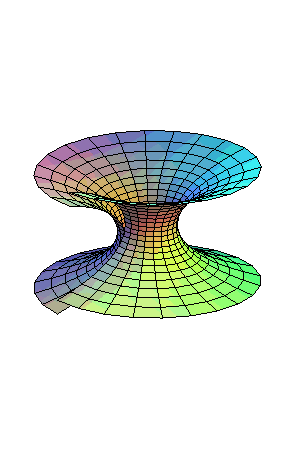
Les hélicoïdes qui sont des surfaces minimales ont la paramétrisation ci-dessus. Ils sont tous localement isométriques entre eux.
Pour a = 0, on obtient le caténoïde, et pour , l'hélicoïde droit.
 

La paramétrisation ci-dessus provient de la paramétrisation de Weierstrass d'une surface minimale : en prenant , , .

Les hélicoïdes minimaux diffèrent donc uniquement par leur angle de Bonnet  ; et l'animation ci-dessus représente en quelque sorte une rotation complexe d'un hélicoïde droit.
 
 

La ligne de coordonnée obtenue pour u = 0 dans la paramétrisation ci-dessus est une hélice circulaire qui est une géodésique de l'hélicoïde minimal ; celui-ci est donc une surface de Björling associée à une hélice circulaire. Dans le cas du caténoïde, l'hélice devient un cercle et dans la cas de l'hélicoïde droit, elle devient l'axe. Les lignes de coordonnée pour v  constant sont des hélices caténoïdiques ; ce sont des génératrices de l'hélicoïde. Dans le cas du caténoïde, elle deviennent des chaînettes, et dans le cas de l'hélicoïde droit, des droites perpendiculaires à l'axe.

 

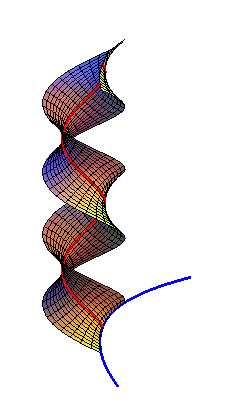surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2011