PARABOLOÏDE ELLIPTIQUE
Elliptic
paraboloid, elliptisches Paraboloid
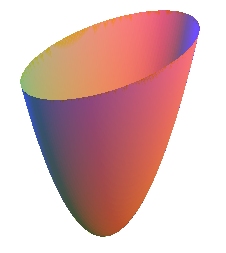
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PARABOLOÏDE ELLIPTIQUE
Elliptic
paraboloid, elliptisches Paraboloid
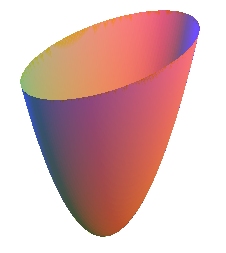
| Équation cartésienne : Quadrique. Paramétrisation cartésienne : Paramétrisation dont les lignes de coordonnées sont les lignes de courbure (cas (figure ci-contre). Courbure de Gauss : |
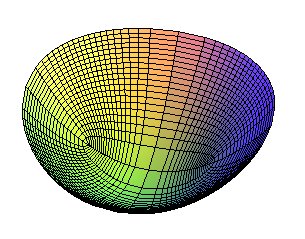 Les projections sur xOy des lignes de courbure
sont les ellipses |
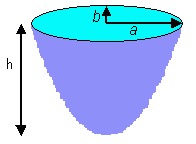
| Volume du bol paraboloïdique de hauteur h,
l'ellipse sommitale ayant pour demi-axes a et b ( |
 |
Les paraboloïdes elliptiques peuvent être définis comme les surfaces engendrées par la translation d’une parabole (ici de paramètre p) le long d’une parabole de même sens (ici de paramètre q) (ce sont donc des surfaces de translation).
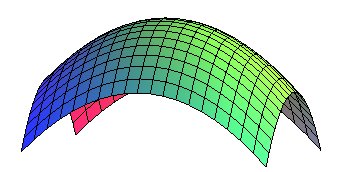
Les sections par des plans verticaux sont des paraboles et les sections par des plans horizontaux sont des ellipses.

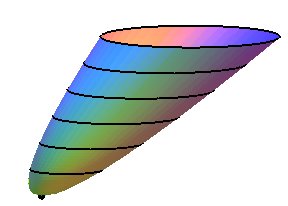 |
Vue de l'une des deux familles de cercles incluse dans tout paraboloïde elliptique, même non de révolution, avec l'ombilic correpondant. |
Le paraboloïde de révolution (ou circulaire) correspond au cas p = q.
Voir à paraboloïde hyperbolique un encadré sur les paraboloïdes confocaux.

Nid d'oiseau en forme de paraboloïde. Si vous avez mieux...
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016