Revolution de la sinusoïde

RÉVOLUTION DE LA SINUSOÏDE
Revolution of the sinusoid, Sinus Drehfläche

Surface étudiée en 2012 par G. Claeser et P. Calvache.
Nom maison, si vous avez mieux, je suis preneur...

Équations cylindrique et cartésienne : et . Paramétrisations cartésiennes :
1) Comme surface de révolution de la sinusoïde autour de Oz : .
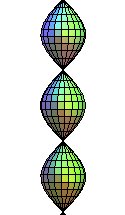2) Comme surface de translation : , lieu des milieux des segments joignant les deux hélice circulaires symétriques : .
3) Comme surface de révolution de l'hélice précédente : .

La révolution de la sinusoïde est la surface de révolution obtenue par la rotation d'une sinusoïde autour de son axe de translation.

Mais il est remarquable que cette surface soit aussi obtenue par translation d'une hélice circulaire sur l'hélice symétrique par rapport à l'axe (comparer avec l'hélicoïde droit qui est obtenu par translation d'une hélice sur elle-même).
Elle est donc aussi obtenue par rotation d'une hélice circulaire autour d'une génératrice du cylindre sur lequel celle-ci est tracée.

La section de cette surface par un cylindre tangent à l'axe et passant par les sommets est donc formée de deux hélices circulaires symétriques.
Remarque de M. de la Palisse : ces hélices sont les... hélices de cette surface de révolution....

Si on trace un réseau régulier de n hélices dextres et n hélices senestres parmi les hélices engendrant la surface, on obtient une structure équivalente au rhombizonoèdre polaire d'ordre n (excepté pour les parties accédant aux sommets). Nicolas Causse appelle ces structures des "zomes-hélices".
Programme maple de tracé de la première figure :
b:=3/4;n:=6;
dextre:=[cos(u+v)*cos(u),sin(u+v)*cos(u),b*u] :
senestre:=[cos(u+v)*cos(u),-sin(u+v)*cos(u),b*u] :
display([seq(tubeplot({dextre,senestre},u=-Pi/2..Pi/2, radius=0.03,grid=[100,20],style=patchnogrid),
v=seq(2*k*Pi/n,k=1..n))],scaling=constrained,axes=none,
orientation=[10,90],lightmodel=light2);
Pour le rhombizonoèdre, il suffit dechanger grid=[100,20] en grid=[n+1,20].
Voir assi la gallerie de Nicolas Causse.

Il existe évidemment d'autres courbes obtenues par révolution d'une sinusoïde, comme par exemple : .

Ne pas confondre avec l'onduloïde, et comparer avec la boite à oeufs.

Voir sur cette page un polyèdre à faces losanges approchant cette surface.

La tour Gherkin à Londres, a été peu ou prou construite sur ce modèle.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres