POIRE DE TANNERY
Tannery's
pear, Tannerische Birne
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POIRE DE TANNERY
Tannery's
pear, Tannerische Birne
| Surface découverte par Tannery en 1892 (bulletin
des sciences mathématiques, page 190).
Jules Tannery (1848 - 1910) : mathématicien français. |
Paramétrisation cartésienne :  ( ).
Équation cylindrique :  .
Première forme quadratique fondamentale :  .
Équation d'une géodésique donnée par  . |
 |
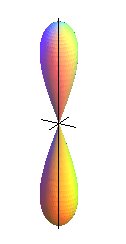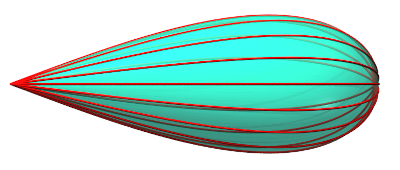
La poire de Tannery est la surface
de révolution engendrée par la rotation autour de son
axe d'une demi-lemniscate
de Gérono ayant subi une affinité de rapport 
(la rotation du huit complet étant parfois appelée "sablier"
de Tannery).
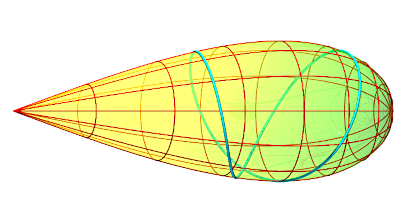
| Il est remarquable que les géodésiques
de cette surface sont fermées, et en forme de huit courbé,
excepté les méridiennes (les surfaces dont les géodésiques
sont fermées sont appelées "surfaces
de Zoll").
De plus, l'équation ci-dessus montre que ce sont
des courbes algébriques, et Tannery a montré qu'elles sont
toutes de même longueur |
 |
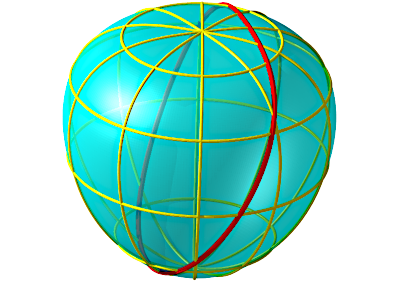
En
1903, Otto Zoll a déterminé une surface dont toutes les
géodésiques sont fermées et de même longueur ,
autre que la sphère, et qui soit de plus lisse, contrairement à
la poire de Tannery :
Paramétrisation cartésienne :  ().
Première forme quadratique fondamentale :  . |
 |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020