binoïde, ou caténoïde

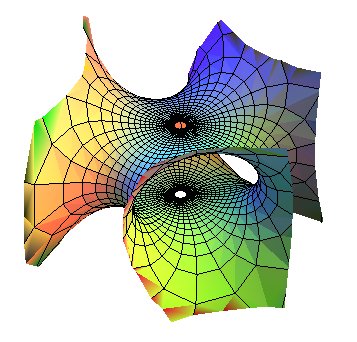
trinoïde

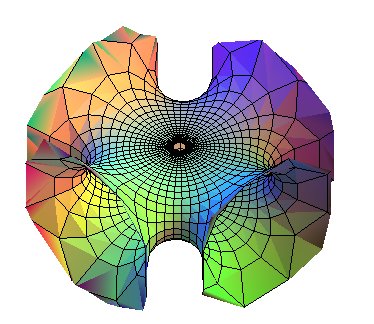
quadrinoïde

 

Surface étudiée par Jorge et Meeks en 1983. Le nom a été formé sur le préfixe tri- et le suffixe -noïde, provenant de "caténoïde".

 

Paramétrisation du trinoïde : [-1/9*(-3*exp(2*u)-3*exp(u)*cos(v)3*exp(3*u)*cos(v)+8*ln(2*exp(u)*cos(v)+ 1+exp(2*u))*exp(2*u)*cos(v)^2+4*ln(-2*exp(u)*cos(v)+ 1+exp(2*u))*exp(u)*cos(v)- 4*ln(4*exp(2*u)*cos(v)^2+ exp(4*u)+ 2*exp(3*u)*cos(v)-exp(2*u) +2*exp(u)*cos(v)+1)*exp(2*u)*cos(v)^2 +2*ln(-2*exp(u)*cos(v)+1+exp(2*u))-ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1)-2*ln(4*exp(2*u)*cos(v)^2+exp(4*u)+2*exp(3*u)*cos(v)-exp(2*u)+ 2*exp(u)*cos(v)+1)*exp(u)*cos(v)+ 4*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(3*u)*cos(v)-2*ln(4*exp(2*u)*cos(v)^2+exp(4*u)+ 2*exp(3*u)*cos(v)-exp(2*u)+ 2*exp(u)*cos(v)+1)*exp(3*u)*cos(v)- 2*ln(-2*exp(u)*cos(v)+1+exp(2*u))*exp(2*u)+ 2*ln(-2*exp(u)*cos(v)+ 1+ exp(2*u))*exp(4*u)+ ln(4*exp(2*u)*cos(v)^2+ exp(4*u)+ 2*exp(3*u)*cos(v)- exp(2*u)+2*exp(u)*cos(v)+1)*exp(2*u)-ln(4*exp(2*u)*cos(v)^2+ exp(4*u)+ 2*exp(3*u)*cos(v)-exp(2*u)+ 2*exp(u)*cos(v)+1)*exp(4*u))/(4*exp(2*u)*cos(v)^2+ exp(4*u)+ 2*exp(3*u)*cos(v)-exp(2*u)+2*exp(u)*cos(v)+1),  1/9*(3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+ exp(u)*cos(v)+1+ exp(2*u))/(exp(u)*cos(v)+1+ exp(2*u)-3^(1/2)*exp(u)*sin(v)))+ 6*exp(2*u)*cos(v)*sin(v)+3*exp(u)*sin(v)-8*3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+ exp(u)*cos(v)+1+exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))*exp(3*u)*cos(v)^3+3*exp(5*u)*sin(v)+3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+exp(u)*cos(v)+1+exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))*exp(6*u)+ 6*3^(1/2)*ln((3^(1/2)*exp(u)*sin(v)+ exp(u)*cos(v)+1+ exp(2*u))/(exp(u)*cos(v)+1+exp(2*u)-3^(1/2)*exp(u)*sin(v)))*exp(3*u)*cos(v)+ 6*exp(4*u)*cos(v)*sin(v))/(1+exp(6*u)+6*exp(3*u)*cos(v)-8*exp(3*u)*cos(v)^3),  2/3*exp(3*u)*(4*cos(v)^3-3*cos(v)-exp(3*u))/(1+exp(6*u)+6*exp(3*u)*cos(v)-8*exp(3*u)*cos(v)^3)]

Le trinoïde, et plus généralement les n-noïdes sont des surfaces minimales ayant une symétrie de rotation d'ordre n et n nappes infinies du type de celle du caténoïde (et ce qu'on pourrait appeler le binoïde n'est d'ailleurs autre que le caténoïde).
On les obtient en prenant  (puis ) dans la paramétrisation de Weierstrass d'une surface minimale : .

Série des n = 2, 3, 4, 5-noïdes, avec bords en pétales, par Alain Esculier.

Ces surfaces se généralisent aux surfaces de courbure moyenne constante (non forcément nulle) ayant une symétrie d'ordre n, voir par exemple ici.
 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2014