Tube

TUBE ou SURFACE TUBULAIRE
Tube or tubular surface or pipe , Röhrenfläche

Tube d'âme un horoptère

Synonyme : surface canal (canal surface, Kanalfläche), tuyau.

Paramétrisation : où et sont les vecteurs normal et binormal à la courbe centrale (G₀) et a le rayon du tube.
Aire de la section : .
Volume de cette section : .

Les tubes de courbe centrale (ou âme, spine curve en anglais) la courbe sont les surfaces cerclées engendrées par un cercle de rayon constant centré sur et dont le plan est constamment normal à cette courbe.
Ce sont aussi les enveloppes d'une sphère de rayon constant centrée sur .
Ce sont les surfaces de Monge de génératrice circulaire.
Le contour apparent d'un tube est formé de deux courbes parallèles à la projection de la courbe centrale.
Exemples : la sphère (cas où est réduit à un point), le cylindre de révolution, le tore, le serpentin.

On peut généraliser la notion de tube dans trois directions :

1) on prend une section non circulaire : on tombe alors sur la notion de surface de Monge, avec une génératrice fermée : Voici par exemple un tube à section carrée :
attention de bien éliminer la torsion pour ne pas tomber dans le cas de droite !

2) on prend un cercle de rayon variable, toujours orthogonal à la courbe centrale : on obtient la notion de tube à section variable.
Exemples :
- les surfaces de révolution
- les tores sinusoïdaux de deuxième espèce. -
Voici par exemple un tube dont la section varie de façon sinusoïdale.

3) on prend des sphères de rayon variable centrées sur , dont on considère l'enveloppe.
Losque est rectiligne, les notions 2) et 3) coïncident, mais pas dans le cas général (cf. ci-contre).
C'est cette notion générale d'enveloppe de sphères de rayon variable qui est parfois désignée par "surface canal" [gray].
La caractérisation est alors : surface cerclée dont les cercles sont des rayons de courbure.
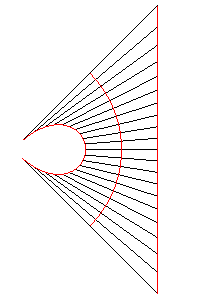Exemple : les cyclides de Dupin. Voici en coupe un tube à section variable engendré par un cercle centré sur un cercle et passant par une droite.
La figure de droite montre que les sphères centrées sur le cercle et tangentes à la droite ne sont pas tangentes à l'autre courbe...

Voir aussi les solénoïdes, enroulements d'un fil autour d'un tube.

Tube à section variable d'âme le cercle (cos t, sin t, 0) et de rayon variable sin t/2 ; le contour apparent est la conchoïde de rosace rho = 1 + sin t/2.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

1) on prend une section non circulaire : on tombe alors sur la notion de surface de Monge, avec une génératrice fermée :	Voici par exemple un tube à section carrée : attention de bien éliminer la torsion pour ne pas tomber dans le cas de droite !
2) on prend un cercle de rayon variable, toujours orthogonal à la courbe centrale : on obtient la notion de tube à section variable. Exemples : - les surfaces de révolution - les tores sinusoïdaux de deuxième espèce.	- Voici par exemple un tube dont la section varie de façon sinusoïdale.
3) on prend des sphères de rayon variable centrées sur , dont on considère l'enveloppe. Losque est rectiligne, les notions 2) et 3) coïncident, mais pas dans le cas général (cf. ci-contre). C'est cette notion générale d'enveloppe de sphères de rayon variable qui est parfois désignée par "surface canal" [gray]. La caractérisation est alors : surface cerclée dont les cercles sont des rayons de courbure. Exemple : les cyclides de Dupin.	Voici en coupe un tube à section variable engendré par un cercle centré sur un cercle et passant par une droite. La figure de droite montre que les sphères centrées sur le cercle et tangentes à la droite ne sont pas tangentes à l'autre courbe...