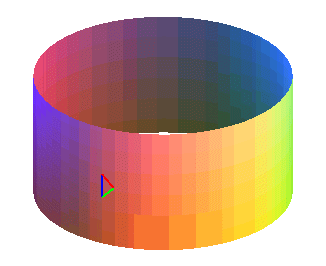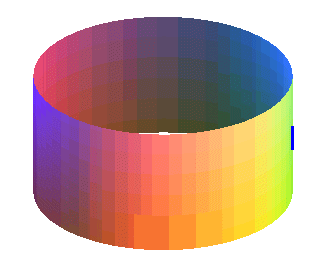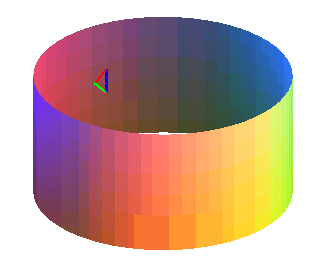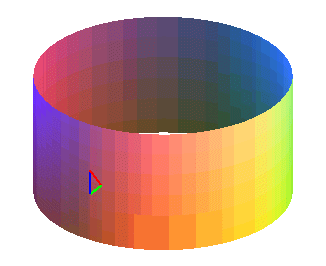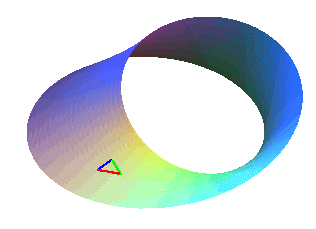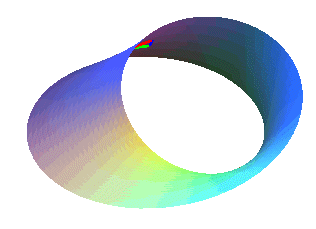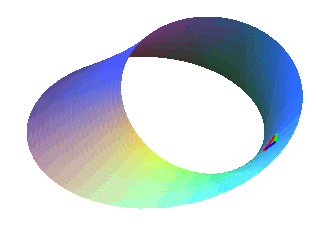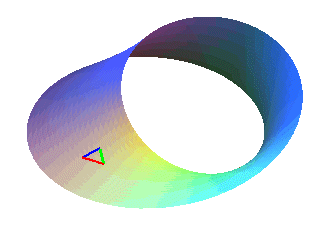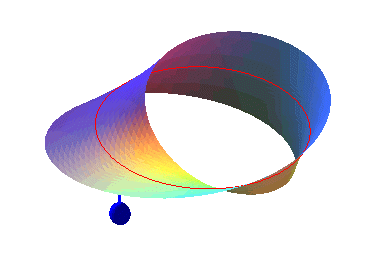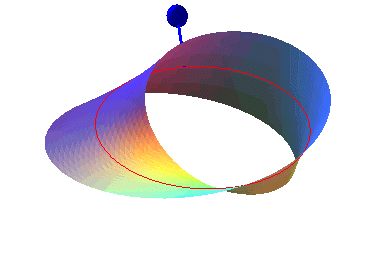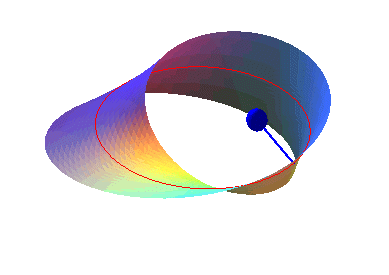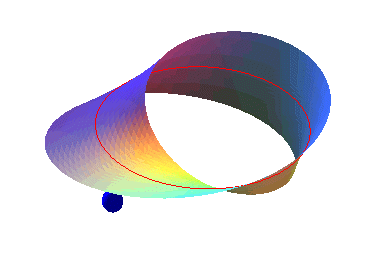Une surface connexe
est dite orientable si l'on ne peut pas amener par déformation continue
un triangle orienté (ABC) inclus dans cette surface
à coïncider avec le triangle orienté dans l'autre sens
(ACB) ; il y a alors deux types d'orientation des triangles.
Dans le cas non orientable, tous les triangles orientés sont superposables.
Par exemple, le ruban "normal" ci-contre est orientable,
alors que le ruban de Möbius
ne l'est pas. |
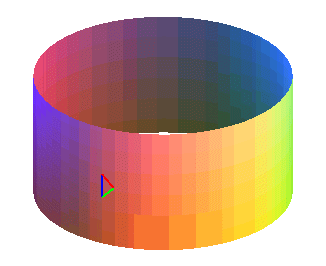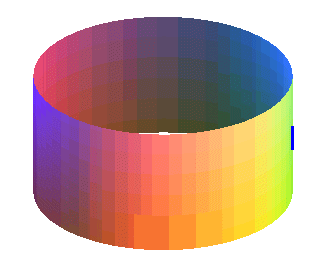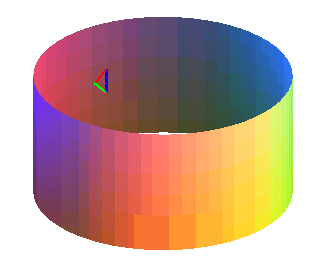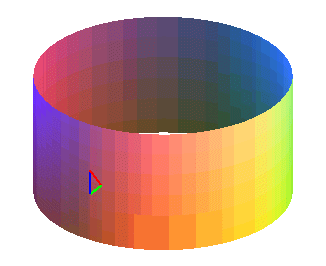
Le triangle garde son orientation.
|
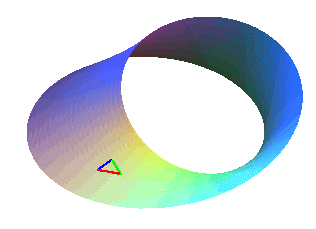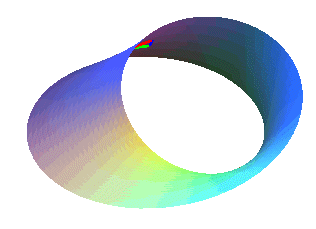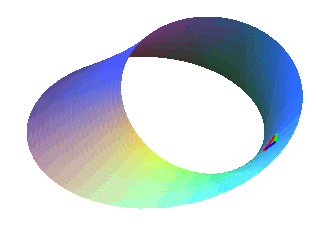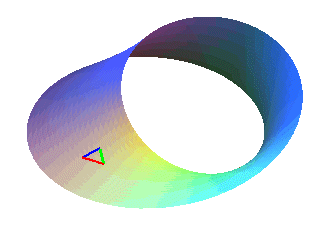
A chaque tour, le triangle change d'orientation ("rouge vert bleu"
devient "rouge bleu vert" ou réciproquement).
|
Plongée dans l'espace euclidien 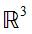 ,
une surface orientable possède deux faces distinctes, que l'on peut
peindre en deux couleurs, ce qui n'est pas le cas des surfaces non orientables,
dites unilatères. Concrètement, pour une surface unilatère,
un observateur placé en un point M d'un certain côté
de la surface, peut, par un mouvement continu, et sans traverser la surface,
se retrouver en M, de l'autre côté. ,
une surface orientable possède deux faces distinctes, que l'on peut
peindre en deux couleurs, ce qui n'est pas le cas des surfaces non orientables,
dites unilatères. Concrètement, pour une surface unilatère,
un observateur placé en un point M d'un certain côté
de la surface, peut, par un mouvement continu, et sans traverser la surface,
se retrouver en M, de l'autre côté. |
 Le "bonhomme" ne peut pas passer de l'autre côté.
Le "bonhomme" ne peut pas passer de l'autre côté.
|
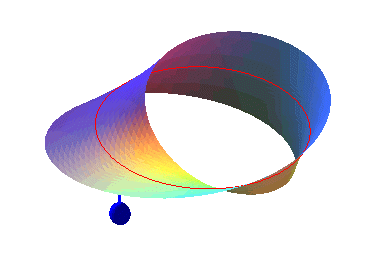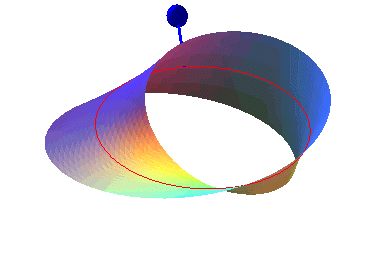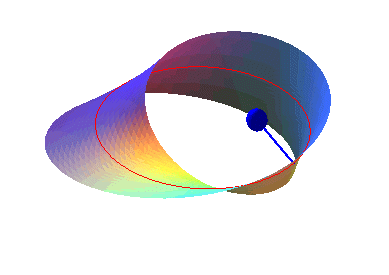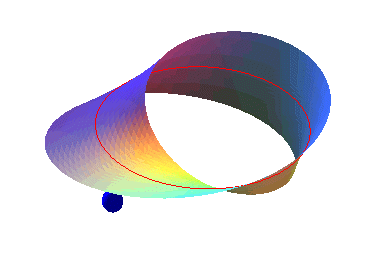
Il peut passer.
|