3D Bézier curve

Curve studied by Bézier in 1954 and by de Casteljau.
Pierre Bézier (1910 - 1999): engineer for Régie Renault.

Affine parametrization: (i.e. ) where the are the Bernstein polynomials: .
Polynomial algebraic curve of degree n.
Curvature at A₀: , torsion at A₀: .

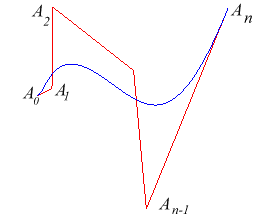Given a broken line (called control polygon, the A_k being the control points), the associated Bézier curve is the curve with the above parametrization; the curve goes through A₀ (for t = 0) and A_n(for t = 1), and the portion that links these points is traced inside the convex hull of the control points; the tangent at A₀is (A₀A₁) and the tangent at A_n is (A_n-1A_n).

Animation of the evolution of a cubic Bézier curve with 4 control points, where A₁ and A₄ are fixed, A₂ and A₃ move on lines.

Recursive construction (de Casteljau algorithm):
The point is the barycenter of and where are the respective current points of the Bézier curves with control points and ; moreover, the line is the tangent at to the Bézier curve.

Conversely, any polynomial 3D algebraic curve is a Bézier curve associated to a unique polygon, once the vertices of the polygon are chosen arbitrarily on the curve.

Their planar conical projections are the plane rational Bézier curves.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

Given a broken line (called control polygon, the A_k being the control points), the associated Bézier curve is the curve with the above parametrization; the curve goes through A₀ (for t = 0) and A_n(for t = 1), and the portion that links these points is traced inside the convex hull of the control points; the tangent at A₀is (A₀A₁) and the tangent at A_n is (A_n-1A_n).
Animation of the evolution of a cubic Bézier curve with 4 control points, where A₁ and A₄ are fixed, A₂ and A₃ move on lines.