CASSINIAN SURFACE

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CASSINIAN SURFACE

| Multipolar equation: Algebraic surface of degree 2n. |
The Cassinian curves with n foci
(or n poles), 3 dimensional analogues of the Cassinian
curves, are the loci of the points in space for which the geometric
mean of their distances to n points is a constant.
|
The case n = 2 gives the surface of revolution with meridian a Cassinian oval. See more details on this page. |
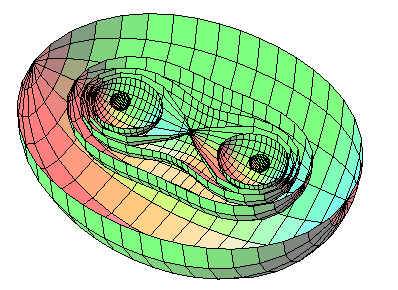 |
If the poles are coplanar, then the section by the plane is a Cassinian curve.
Below are some examples of Cassinian surfaces the poles
of which are located at the vertices of a regular polyhedron with radius
a.
| Poles at the vertices of a tetrahedron.
Various views when b/a increases from 0,9 to 2. |
 |
 |
 |
 |
 |
| Poles at the vertices of an octahedron.
Various views when b/a increases from 1 to 1.6. |
 |
 |
 |
| Poles at the vertices of a cube.
Various views when b/a increases from 1 to 2. |
 |
 |
 |
| Poles at the vertices of an icosahedron; for the dodecahedron, see the figure at the top. |
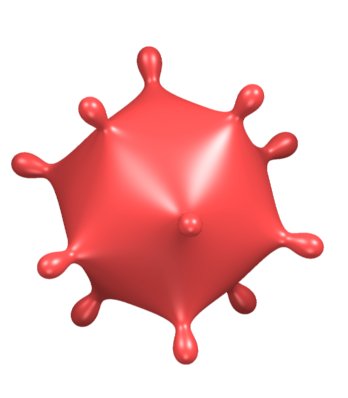 |
See also the Cassini surfaces.


| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017