CONCHAL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CONCHAL

| Curve studied by Schlömilch in 1878 and G. Huber
in 1895.
From the Latin Cochlea, itself coming from the Greek kokhlias: shell, snail (cf. the cochlea in the internal ear and the cuiller, instrument used to eat snails). K. Fladt p. 236. |
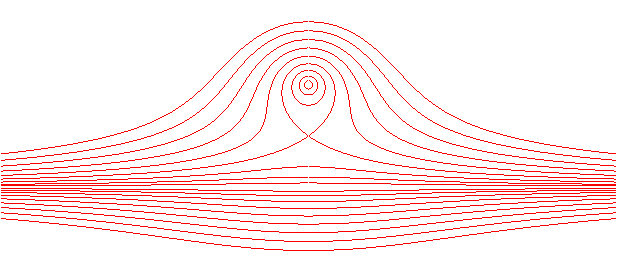
| Cartesian equation: Circularquartic, rational if c = a. |
The conchals are the loci of the points for which the product of their distances to a fixed point (here (F(–a, 0)) and to a fixed line (here x = a) is constant: MF MH = c2.
The curves assume the following aspects:
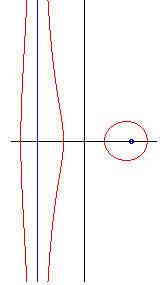
| When 0 < c < a, we get two infinite
branches for which the line x = –a is the asymptote when |
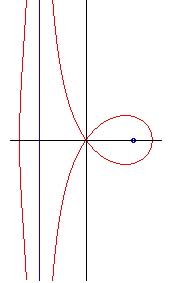
When c = a (O is a double point,
the curve is rational): we get two infinite branches for which x
= –a is the asymptote, the second having a loop, when |
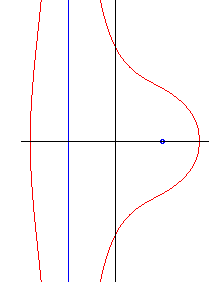
For c > a, we get two infinite branches
for which the line x = –a is the asymptote, when |
 |
 |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017