| bibliographie | introduction | retour accueil | courbes 2D | courbes 3D | fractals | polyèdres |
|
|
|
Surfaces commençant par
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ALLONGÉ (ELLIPSOÏDE DE RÉVOLUTION/)
APLATI (ELLIPSOÏDE DE RÉVOLUTION/)
ARÊTE DE REBROUSSEMENT D'UNE SURFACE RÉGLÉE DÉVELOPPABLE
ASYMPTOTIQUE D'UNE GÉNÉRATRICE DE SURFACE RÉGLÉE (PLAN/)
ATTRACTION MAXIMALE (SOLIDE D'/)
BISPHÉRIQUE (SURFACE ALGÉBRIQUE/)
CARACTÉRISTIQUE D'EULER-POINCARÉ D'UNE VARIÉTÉ, D'UNE SURFACE
CATALAN (SURFACE MINIMALE DE/)
CENTRAL D'UNE GÉNÉRATRICE DE SURFACE RÉGLÉE (POINT/)
CHROMATIQUE D'UNE SURFACE (NOMBRE/)
CLEBSCH (SURFACE (CUBIQUE) DE/)
CÔNE OU SURFACE CONIQUE
COURBURE DE GAUSS CONSTANTE (SURFACE DE RÉVOLUTION À/)
COURBURE MOYENNE CONSTANTE (SURFACE DE RÉVOLUTION À/)
COURBURE PLANES (SURFACE À LIGNES DE /)
CYLINDROÏDE
DARBOUX (CYCLIDE DE/)
DEVELOPPANTE D'UNE SURFACE DÉVELOPPABLE
DIRECTRICE RECTILIGNE (SURFACE RÉGLÉE À/)
DYCK (SURFACE DE/)
ÉGALE PENTE (SURFACE D'/)
ÉLASTICITE DE FRESNEL (SURFACE D'/)
ELLIPTIQUE (POINT / D'UNE SURFACE)
ENVELOPPE D'UNE FAMILLE DE SURFACES
EULER-POINCARÉ
D'UNE VARIÉTÉ, D'UNE SURFACE (CARACTÉRISTIQUE D'/)
FILET D'EAU (SURFACE DU/)
FRESNEL (SURFACE D'ÉLASTICITÉ DE/)
FRESNEL (SURFACE DES ONDES DE/)
GYROÏDE
HABILLAGE DE LA SPHÈRE
HYPERBOLIQUE (POINT / D'UNE SURFACE)
HYPERBOLOÏDE
À
UNE NAPPE (H1)
À
DEUX NAPPES (H2)
HYPERSPHÈRE (de dimension 3, de dimension n)
HYPERTORE
INDICATRICE
DE DUPIN
INVERSE D'UNE SURFACE PAR RAPPORT A UNE SPHÈRE
ISOMÉTRIQUE (SURFACE / A UNE AUTRE)
LARGEUR CONSTANTE (SURFACE DE/)
LIGNE TRACÉE SUR
UNE SURFACE
LIGNE
DE
COURBURE,
ASYMPTOTIQUE,
GÉODÉSIQUE
LIGNE TOPOGRAPHIQUE
:
DE
NIVEAU,
DE PENTE,
DE
TALWEG,
DE FAÎTE,
LISSE (SURFACE/)
MÉPLAT (D'UNE SURFACE)
MÉRIDIENNE (OU MÉRIDIEN) D'UNE SURFACE DE RÉVOLUTION
MOULURE (SURFACE/)
NADIRASHVILI
(SURFACE DE/)!
ONDES (SURFACE DES / DE FRESNEL)
OVOÏDE
PARABOLE
(RÉVOLUTION DE LA / AUTOUR D'UN AXE PARALLELE A LA DIRECTRICE)
PARABOLIQUE (POINT / D'UNE SURFACE)
PARALLÈLE (SURFACE / A UNE AUTRE)
PENTE (LIGNE DE/, ou LIGNE DE PLUS GRANDE/)
PLI (SURFACE DEVELOPPABLE AVEC/)
POLAIRE D'UNE COURBE GAUCHE (SURFACE/)
POLAIRE (RÉCIPROQUE) D'UNE SURFACE, D'UNE COURBE PAR RAPPORT A UNE SPHÈRE
PRESSION CONSTANTE (SURFACE DE LA TOUR À/)
RÉVOLUTION AUX COURBURES PROPORTIONNELLES (SURFACE DE)
RIEMANN (SURFACE MINIMALE DE/)
RIEMANN (SURFACE MINIMALE FINIE DE/)
SCHWARZ (SURFACES MINIMALES DE/)
SOMME CONNEXE DE DEUX SURFACES
STRICTION D’UNE SURFACE RÉGLÉE NON DÉVELOPPABLE (LIGNE DE/)
SYMÉTRIE DE ROTATION (SURFACE À/)
SYSTEME TRIPLE ORTHOGONAL
(DE SURFACES)
TAKAGI (MONT/)
TÉTRAÉDRIQUE (SURFACE / DE KUMMER)
TRIPLE ORTHOGONAL (SYSTÈME/ DE SURFACES)
TUBE ou SURFACE TUBULAIRE
UNILATÉRE (SURFACE)
VARIÉTÉ (topologique, différentielle, algébrique)
VIS À FILET CARRÉ (SURFACE DE LA/)
VIS À FILET TRIANGULAIRE (SURFACE DE LA/)
(S) surface en cours d’étude.
M : point courant de la surface.
(O, 
,
,
)
repère orthonormé direct, d’axes Ox , Oy et
Oz.
(x, y, z) : coordonnées cartésiennes de M.
:
coordonnées cylindriques (ou semi-polaires) de M ; 
.
ou 
:
coordonnées sphériques de M (
est la longitude, 
est
la latitude et 
la colatitude).
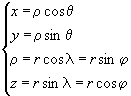
Généralisation aux coordonnées toriques
(r, r, q,l)
:
u, v : paramètres.
Équation, paramétrisation cartésiennes : caractérisation en x, y et z.
Équation, paramétrisation cylindriques :
caractérisation en r, et
z.
Équation, paramétrisation sphériques : caractérisation en r, q et l.
, 
, 
,
,
.
,
, 
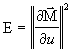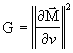: coefficients de la première forme quadratique fondamentale
(s = abscisse curviligne d'une courbe tracée sur la surface)
:
.
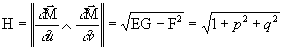: élément d’aire.
: vecteur normal.
, 
, 
:
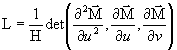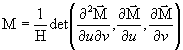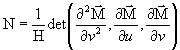coefficients de la deuxième forme quadratique
fondamentale :
R1et R2 : rayons de courbure principaux (i. e. extrémaux) en M.
et 
: courbures
principales en M.
: courbure de Gauss (ou totale) en M.
Attention : l'expression "courbure totale" est plutôt
utilisée pour l'intégrale de la courbure de Gauss
sur la surface.
: courbure moyenne en M.
.
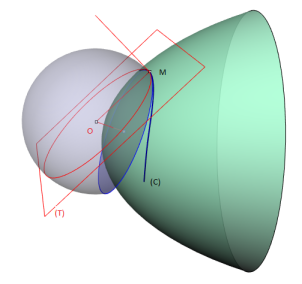
FORMULES CONCERNANT UNE COURBE TRACÉE SUR UNE SURFACE
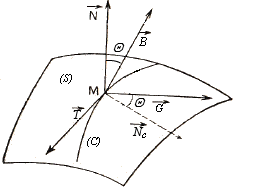
Soit (C) une courbe tracée sur (S)
passant par M , de trièdre
de Frenet
.
Le trièdre de Darboux-Ribaucour (ou géodésique)
est 
où
.
,
angle de la rotation faisant passer de Frenet à Darboux, angle entre
le plan osculateur à la courbe et le plan tangent à la surface
:
.
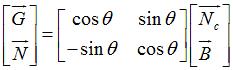
Formules de Frenet : 
;
formules de Darboux : 
,
: rayon de courbure normal (rayon de courbure de la section normale de
la surface tangente à la courbe), 
: courbure normale.
 : rayon
de courbure géodésique (rayon de la sphère qui contient
le cercle osculateur de la courbe et dont le centre se trouve sur le plan
tangent à la surface). C'est aussi le rayon de courbure de la courbe
projetée de la courbe de départ sur le plan tangent à
la surface. |
 |
: courbure géodésique ; c'est la courbure des deux lignes
asymptotiques passant par M. On a 
.
:
rayon de torsion géodésique ; 
: torsion géodésique ; c'est la torsion des lignes asymptotiques,
et des géodésiques
passant par M (ainsi que des pseudo-géodésiques).
Soit 
l’angle entre la première
direction principale et la tangente à (C) ; on a la
formule d'Euler : 
, et la formule de Bonnet :
,
et 
.
| bibliographie | introduction | Retour accueil | courbes 2D | courbes 3D | fractals | polyèdres |