
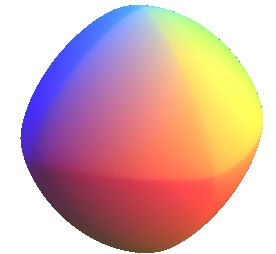
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE LAMÉ
Lamé
surface, Lamesche Fläche

|

|
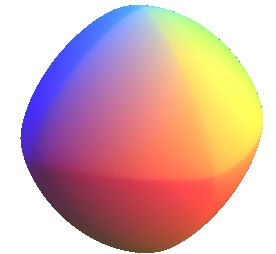
|
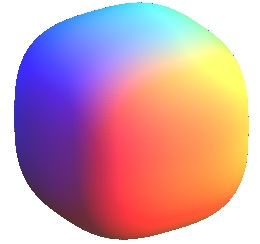
|
|
| Gabriel Lamé (1795-1870) : ingénieur et
mathématicien français.
Autres noms : superellipsoïde, surface quasi ellipsoïdale. |
| Equation cartésienne de Paramétrisation cartésienne : Volume de la boule associée : |
La surface de Lamé
est la "sphère" de rayon 1 associée à la norme
;
Pour un rationnel ,
la surface
,
partie de
intersectée avec le huitième d'espace
est une portion de surface algébrique notée
de degré ?? ; lorsque p est pair,
et
coïncident.
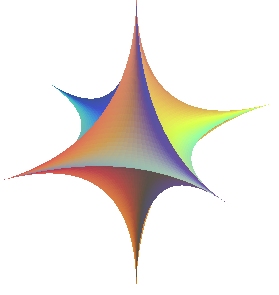
Exemples de surfaces de Lamé avec a = b
=
c
:
| surface octaédrale |
plan | |
| sphère : |
même sphère | |
| surface quartique |
||
| surface astroïdale | surface de degré 18 |
Ces surfaces se généralisent en les hypersurfaces
de dimension n d'équation
dont le volume de la boule associée vaut
; le cas n = 2 donne bien sûr les courbes
de Lamé.
Par exemple, le cas ,
,
donc d'équation
,
donne la surface de l'hyperoctaèdre
de dimension n.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2021