COURBES 2D
Voir les notations
ci-dessous.
Courbes commençant par
Classification par l'équation polaire :
Familles de courbes en polaires :
Classification par l'équation cartésienne explicite en
y
(courbes
algébriques) :
Classification par la forme :

cubique d'Agnesi, visiera,
cubique
de Lamé, courbe de Gauss, sécantoïde
hyperbolique
|

parabole, chaînette,
chaînette
d'égale résistance
|

cissoïde, parabole
semi-cubique, tractrice, développante
de parabole, conchoïde
de droite
|

strophoïde,
cubique
de Tschirnhausen,
trisectrice de
Maclaurin, folium
de Descartes
|
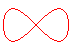
lemniscates
|

sinusoïde, lintéaire,
roulette
de Sturm
|
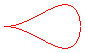
quartique piriforme, larme
|

spirales
|
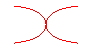 
kappa, puntiforme
|
Définitions géométriques à partir de deux
pôles A et B.
Définitions géométriques à partir d'un pôle
A
et d'une droite (D) ; H est le projeté de
M
sur (D).
Définition par l'équation intrinsèque
1
ABDANK-ABAKANOWICZ (QUADRATRICE D'/)
ACCÉLÉRATION
ANGULAIRE CONSTANTE (COURBE À/)
AGNESI (CUBIQUE D'/)
ALAIN (COURBE D'/)
AILE D'AVION (PROFIL D'/)
ALGÉBRIQUE (COURBE)
ALLONGÉE (CYCLOÏDE,
ÉPICYCLOÏDE,
HYPOCYCLOÏDE)
ALLONGÉE (CISSOÏDE)
ALYSOÏDE
AMORTIE (PARABOLE)
ANALLAGMATIQUE (COURBE/)
ANALLAGMATIQUE
(SPIRALE/)
ANAMORPHOSE
ANE (COURBE DE L'/)
ANGUINEA
ANGUINÉE
ANSE DE PANIER
ANTICAUSTIQUE
ANTI-CLOTHOÏDE
ANTIHYPERBOLISME D'UNE
COURBE
ANTILOGA
ANTIPARALLÉLOGRAMME
ARTICULÉ (COURBE DE L')
ANTIPODAIRE
APIENNE (cresci + crdp + Loria p. 238)
APLANÉTIQUE (COURBE/)
APOLLONIUS (CUBIQUE D'/)
ARACHNÉE
ARAIGNÉE
ARCHIMÈDE (SPIRALE D'/)
ASTROÏDE
ATRIPHTHALOÏDE
AUTOPARALLÈLE
(COURBE/)
AXÉE (CUBIQUE
CIRCULAIRE/)
BÂCHETTE
BALISTIQUE (COURBE/)
BARYCENTRIQUE
BASE D'UN MOUVEMENT PLAN SUR PLAN
BASE DU SYSTEME BIELLE-MANIVELLE
BÉRARD (COURBE
DE LA BIELLE DE/ )
BERNOULLI (LEMNISCATE DE/)
BERNOULLI (SPIRALE DE/)
BESACE
BÉZIER (COURBE DE/)
BÉZIER
RATIONNELLE (COURBE DE/)
BICIRCULAIRE (COURBE ALGÉBRIQUE/)
BICORNE
BIELLE DE BÉRARD
(COURBE DE LA/)
BIFOLIUM
BIFOLIUM DROIT
BIFOLIUM RÉGULIER
BIQUARTIQUE
BITOÏDE
BLANC-MANGER
(COURBE DU/)
BOOTH (COURBE, LEMNISCATE, OVALE DE/)
BOWDITCH (COURBE DE/)
BOUCHE
BRACHISTOCHRONE (COURBE/)
BRACHISTOCHRONE
DE LONGUEUR DONNÉE (COURBE/)
BROCARD (TRANSFORMATION DE)
BROWNIEN
(COURBE DU MOUVEMENT/)
B-SPLINE (COURBE/)
CACAHUÈTE
CAMPYLE D'EUDOXE
CAPPA
CAPRICORNOÏDE Loria p. 336
CAQUOÏDE
CARDIOÏDE
CARTÉSIENNE
CASSINI (OVALE DE/)
CASSINIENNE
CATACAUSTIQUE
CATALAN (COURBE DE/)
CATALAN (TRISECTRICE
DE/)
CATOPTRICE
CAUSTIQUE
CAUSTIQUE
INVERSE
CAUSTIQUE DE CERCLE
CAYLEY (SEXTIQUE DE/)
CAYLEY (OVALE DE/)
CERCLE
CEVA (TRISECTRICE
DE/)
CHAÎNE SUSPENDUE
(COURBE DE LA/)
CHAÎNETTE
CHAÎNETTE
D’ÉGALE RÉSISTANCE
CHAÎNETTE ÉLASTIQUE
CHAÎNETTE ELLIPTIQUE, HYPERBOLIQUE
CHAMP (LIGNES DE)
CHIEN (COURBE DU)
courant vers
son maître
tirant sur
sa laisse
nageant dans le
courant
CIRCULAIRE (COURBE ALGÉBRIQUE/)
CISSOÏDALE (COURBE/)
CISSOÏDALE
DE ZAHRADNIK
CISSOÏDE
CISSOÏDE DE DIOCLÈS
CISSOÏDE DROITE
CLAIRAUT (COURBE DE/)
CLINOÏDE
CLOCHE (COURBE EN/)
CLOTHOÏDE
COCHLÉOÏDE
COEUR
CONCHALE
CONCHOÏDE
CONCHOÏDE
DE CERCLE
CONCHOÏDE DE DÜRER
CONCHOÏDE
DE NICOMÈDE
CONCHOÏDE
DE ROSACE
CONCHOÏDE FOCALE
DE CONIQUE
CONIQUE
CONTOUR APPARENT
D'UNE SURFACE
CONTRE-PODAIRE
CORDE À SAUTER (COURBE
DE LA/)
CORNOÏDE
CORNU (SPIRALE DE/)
COTES (SPIRALE DE/)
COURBE
CRABE (COURBE DU)
CRAMER (TRIFOLIUM DE/)
CRANIOÏDE Loria p. 334
CROIX DE MALTE
CRUCIFORME
CUBIQUE
CUBIQUE (PARABOLE/)
CUBIQUE D'AGNESI
CUBIQUE D'APOLLONIUS
CUBIQUE DE CHASLES
CUBIQUE CIRCULAIRE
CUBIQUE CIRCULAIRE
AXÉE
CUBIQUE CIRCULAIRE
FOCALE
CUBIQUE
CIRCULAIRE RATIONNELLE
CUBIQUE
CIRCULAIRE RATIONNELLE DROITE
CUBIQUE DUPLICATRICE
CUBIQUE ELLIPTIQUE
CUBIQUE ISOPTIQUE
CUBIQUE DE LAME
CUBIQUE MIXTE
CUBIQUE RATIONNELLE
CUBIQUE DE SLUZE
CUBIQUE DE TSCHIRNHAUSEN
CUBOCYCLOÏDE
CYCLIQUE
CYCLOÏDALE (COURBE/)
CYCLOÏDE
CYCLOÏDE ALLONGÉE,
RACCOURCIE
CYCLOÏDE À
CENTRE
DANSEUR DE CORDE (COURBE DU/)
DE BEAUNE
(COURBE DE/) (cf. aussi Brocard Lemoine Tome II, p.28)
DÉFÉRENTE
DELAUNAY (ROULETTE DE/)
DELANGES (TRISECTRICE DE/)
DELTOÏDE
DENTELEE
DESCARTES (FOLIUM
DE/)
DESCARTES (OVALE DE/)
DESCARTES (PARABOLE DE/)
DÉVELOPPANTE D'UNE
COURBE
DÉVELOPPANTE
DE CERCLE
DÉVELOPPANTE
D'EXPONENTIELLE
DÉVELOPPANTE
SOMMITALE DE PARABOLE
DÉVELOPPANTE
OBLIQUE D'UNE COURBE
DÉVELOPPÉE D'UNE
COURBE
DÉVELOPPÉE
OBLIQUE D'UNE COURBE
DÉVELOPPOÏDE
DÉVELOPPOÏDE
INVERSE D'UNE COURBE
DIABLE (COURBE DU)
DIACAUSTIQUE
DINOSTRATE (QUADRATRICE DE/)
DIOCLES (CISSOÏDE
DE/)
DIPÔLE (COURBE DU/)
DIVERGENTE
(PARABOLE/)
DOPPLER (SPIRALE/)
DOUBLE COEUR
DOUBLE GOUTTE D'EAU
DOUBLE U
DROITE
DROITE (CISSOÏDE/,
STROPHOÏDE/)
DUPLICATRICE
DUPORCQ (COURBE DE/)
DÜRER (CONCHOÏDE DE/)
DÜRER (FOLIUM DE/)
ECLAIREUR (COURBE DE L'/)
ÉLASTIQUE (COURBE/)
ELLIPSE
ELLIPTIQUE (COURBE/)
ENGRENAGE
ENVELOPPE D'UNE FAMILLE DE COURBES
PLANES
ÉPI
ÉPICYCLOÏDE
ÉPICYCLOÏDE ALLONGÉE,
RACCOURCIE
ÉPITROCHOÏDE
ÉQUIDISTANCE (COURBE
D'/)
ÉQUIANGLE (SPIRALE/)
ÉQUILATÈRE (HYPERBOLE/)
ÉQUIPOTENTIELLE (COURBE/)
ÉQUITANGENTIELLE
(COURBE/)
ESPERLUETTE (COURBE
DE L')
ÉTOILE DE
MER
EUDOXE (KAMPYLE D'/)
EULER (SPIRALE D')
EXPONENTIELLE (COURBE)
FERMAT (COURBE DE/)
FERMAT (SPIRALE DE/)
FIBONACCI (SPIRALE DE/)
FILATURE
FLEUR DE JASMIN
FLECHES (COURBE À/)
FOCALE DE QUÉTELET
FOCALE DE VAN REES
FOLIOÏDE
FOLIUM
FOLIUM DE DESCARTES
FOLIUM DE DÜRER
FOLIUM DOUBLE
FOLIUM DROIT
FOLIUM PARABOLIQUE
FOLIUM SIMPLE
FORCATS (COURBE DES/)
FRONTS D'ONDES
FREETH (NÉPHROÏDE
DE/)
FUNICULAIRE (COURBE/)
GALILÉE (SPIRALE DE/)
GAUSS (COURBE DE/)
GÉNÉRIQUE (COURBE/)
GENRE D'UNE COURBE ALGÉBRIQUE
GERONO (LEMNISCATE DE/)
GIRATION (COURBE DE/)
GLISSETTE
GLISSETTE
TANGENTIELLE
GOURSAT (COURBE DE/)
GOUTTE D'EAU
GUTSCHOVEN (COURBE DE/)
HÉLICE DE BATEAU
HIPPIAS (SECTRICE D'/)
HIPPOPÈDE DE PROCLUS
HIRE (COURBE DE LA/)
HOLDITCH (COURBE DE)
HOROCYCLE
HUIT
HUMBERT
HYPERBOLE
HYPERBOLE CUBIQUE
HYPERBOLE ÉQUILATÈRE
HYPERBOLIQUE (SPIRALE/)
HYPERBOLISME D'UNE COURBE
HYPERCYCLOÏDE
HYPOCYCLOÏDE
HYPOCYCLOÏDE ALLONGÉE,
RACCOURCIE
HYPOCYCLOÏDE DE STEINER
HYPOTROCHOÏDE
INFLEXION (COURBE À LONGUE/)
INTÉGRALE DE CERCLE
INVERSE BIAXIAL DE HUIT
INVERSE D'UNE COURBE PAR RAPPORT
A UN POINT
ISOCHRONE DE HUYGENS
ISOCHRONE DE LEIBNIZ
ISOCHRONE PARACENTRIQUE (gomes, loria)
ISOCHRONE DE VARIGNON
ISOCONCHOÏDE
DE DROITE
ISOCLINE
ISOÉNERGIE DU PENDULE PESANT
(COURBES D'/)
ISOPHONIQUE (COURBE/)
ISOPTIQUE (COURBE/)
ISOPTIQUE (CUBIQUE/)
ISOTRÉPENTE (COURBE/)
ISOTÈLE (COURBE/)
JASMIN (FLEUR
DE/)
JERABEK (COURBE DE/)
JET D'EAU (COURBE
DU/)
JORDAN
(COURBE DE/)
JOUE COURBE D'ALICE
JOUKOVSKI (COURBE DE/)
KAMPYLE D'EUDOXE
KAPPA
KEPLER (OEUF DE/)
KIEPERT (COURBE DE/)
KIEROÏDE
KLEIN (QUARTIQUE DE/)
KÜLP (QUARTIQUE DE/)
LAGRANGE (COURBE D'INTERPOLATION
DE/)
LA HIRE (COURBE, DROITE, ENGRENAGE
ou MOUCHE DE/)
LAMÉ (COURBE DE/)
LAPINS (OREILLES DE/)
LARGEUR CONSTANTE
(COURBE DE/)
LARME
LEMNISCATE
LEMNISCATE DE BERNOULLI
LEMNISCATE DE BOOTH
LEMNISCATE DE GERONO
LEMNISCATE
À n FOYERS (ou n POLES/)
L'HOSPITAL (CUBIQUE DE/)
L'HOSPITAL
(QUINTIQUE DE/)
LIGNE DE CHAMP
LIMAÇON DE PASCAL
LIMAÇON TRISECTEUR
LINTÉAIRE
LINTÉAIRE DROITE
LION (COURBE DU)
LISSAJOUS (COURBE OU FIGURE DE/)
LISSE (COURBE/)
LITUUS
LOGARITHMIQUE (COURBE/)
LOGARITHMIQUE (SPIRALE/)
LOGOCYCLE
LOG
COSINUS (COURBE DU/)
LOOPING
(COURBE DU/)
LORIGA (COURBE DE/)
MACLAURIN (TRISECTRICE DE/)
MAGNÉTIQUE
INDUIT PAR UNE SPIRE CIRCULAIRE (LIGNE DE CHAMP/)
MANNHEIM (COURBE DE/)
MASCOTTE (COURBE DE LA/)
MÉANDRES (COURBE DES/)
MÉDIANE (COURBE/)
MÉDIATRICE (COURBE/)
MÉTACENTRIQUE
D'UN PROFIL DE NAVIRE (COURBE/)
MONGE (CERCLE DE/)
MOULIN À VENT
MOUVEMENT PLAN SUR PLAN
MULTICARDIOÏDE
MULTICIRCULAIRE (COURBE/)
MULTIELLIPSE
MULTIFOCALE (ELLIPSE)
MULTIFOLIUM
NAGEUR (COURBE DU/)
n CENTRES (SPIRALE A/)
NEILE (PARABOLE
DE/)
NÉPHROÏDE
NÉPHROÏDE DE
FREETH
NEWTON (STROPHOÏDE
DE/)
NEWTON (TRANSFORMATION
DE/)
NEWTON (TRIDENT DE/)
NICOMÈDE
(CONCHOÏDE DE/)
NIVEAU (LIGNE OU
COURBE DE/)
NŒUD
NŒUD PAP
NORWICH (SPIRALE DE/)
NORWICH (SPIRALE DE/ INVERSE)
n-SECTRICE
OBLIQUE (CISSOÏDE OU STROPHOÏDE/)
OEUF D'EHRHART
OEUF DE GRANVILLE
OEUF DE HÜGELSCHÄFFER
ŒUF DE KEPLER
OEUF DOUBLE
OPHIURIDE
OR (SPIRALE D'/)
ORBIFORME
ORNEMENTALES (COURBES/)
ORTHOCAUSTIQUE
ORTHOCONCHOÏDE
DE DROITE
ORTHOGONALE (TRAJECTOIRE/)
ORTHOPOLAIRE (COURBE/ D'UNE
COURBE PAR RAPPORT A DEUX DROITES)
ORTHOPTIQUE (COURBE/)
ORTHOTOMIQUE (COURBE/)
OVALE
OVALE DE CASSINI
OVALE DE CAYLEY
OVALE DE DESCARTES
PAPILLON
PARABOLE
PARABOLE AMORTIE
PARABOLE CUBIQUE
PARABOLE DE DESCARTES
PARABOLE DIVERGENTE
PARABOLE DE NEILE
PARABOLE SEMI-CUBIQUE
PARABOLIQUE (SPIRALE/)
PARACENTRIQUE (COURBE
(ISOCHRONE)/)
PARACYCLOÏDE
PARALLÈLE (COURBE/)
PENDULE (COURBES D'ISOÉNERGIE
DU/)
PÉRICYCLOÏDE
PERITROCHOÏDE
PERLE DE SLUZE loria p. 376
PINOCHOÏDE
PIRIFORME (QUARTIQUE/)
PLAN SUR PLAN (COURBES ASSOCIÉES
A UN MOUVEMENT /)
PLÜCKER (QUARTIQUE
DE/)
PODAIRE
POINSOT (SPIRALE DE/)
POISSON
POLAIRE (RÉCIPROQUE) D'UNE
COURBE PAR RAPPORT A UN CERCLE
POLYGASTÉROÏDE
POLYNOMIALE (COURBE/)
POLYZOMALE (COURBE/)
POLYTROCHOIDE
PONT-LEVIS (COURBE DU/)
PONT SUSPENDU
PORTE D’AUTOBUS (COURBE DE LA/)
POURSUITE (COURBE DE/)
POURSUITES MUTUELLES
(COURBE DE/)
POURSUITE PARALLÈLE
(COURBE DE/)
PRESSION CONSTANTE
(PROFIL DE LA TOUR À/)
PROFIL CONJUGUÉ
PSEUDO-CYCLOÏDALE
(COURBE)
PSEUDO-SPIRALE DE PIRONDINI
PTÉROIDE
PUNTIFORME
QUADRATRICE
QUADRATRICE D'ABDANK-ABAKANOVICZ
QUADRATRICE DE DINOSTRATE
QUADRICUSPIDE
QUADRIFOLIUM
QUARTIQUE
QUARTIQUE
BICIRCULAIRE
QUARTIQUE
BICIRCULAIRE RATIONNELLE
QUARTIQUE DE KLEIN
QUARTIQUE DE LORIGA
QUARTIQUE PIRIFORME
QUARTIQUE DE PLÜCKER
QUARTIQUE DE TROTT
QUARTIQUE RATIONNELLE
QUARTIQUE DE RUIZ-CASTIZO
QUATRE-BARRES (COURBE DU)
QUATRE CENTRES (SPIRALE
A/)
QUINTIQUE
QUINTIQUE
DE L'HOSPITAL
RACCOURCIE (CYCLOÏDE/,
ÉPICYCLOÏDE/,
HYPOCYCLOÏDE/)
RADIALE D’UNE COURBE
RADIOÏDE
RAMPHOÏDE
RAYON SINUSOÏDAL (COURBE
À/)
RATIONNELLE (COURBE/)
RÉACTION
CONSTANTE (COURBE À/)
REES (FOCALE DE VAN/)
RÉFRACTION (CAUSTIQUE PAR/)
REPTOIRE
RHODONNÉE
RIBAUCOUR (COURBE DE/)
ROLLE (COURBE DE /) crdp p.34 bouasse 329 et 259 loria
p. 92
ROSE DE GRANDI
ROSACE
ROSACE DE TROIE
ROSILLO (COURBE DE/)
ROUE ET ROUTE
ROUE DENTÉE
ROULANTE
ROULETTE
ROULETTE
À BASE ELLIPTIQUE D'ELLIPSE
ROULETTE À
BASE RECTILIGNE
ROULETTE À
BASE RECTILIGNE D'ELLIPSE
ROULETTE DE DELAUNAY
ROULETTE DE STURM
RUIZ CASTIZO (QUARTIQUE
DE/)
SALKOWSKI
(COURBE DE)
SALMON (QUARTIQUE DE)
SCARABÉE
SCYPHOÏDE
SEAU D'EAU (COURBE
DU/)
SÉCANTOÏDE
SECANTOÏDE HYPERBOLIQUE
SECTRICE
SECTRICE DE MACLAURIN
SELMER
(CUBIQUE DE/)
SEMI-CUBIQUE
(PARABOLE/ OU COURBE/)
SEMI-TRIDENT
SEPTIQUE
SERPENTINE (CUBIQUE/)
SERPENTINE DROITE
1
SERPENTINE DROITE
2
SEXTIQUE
SEXTIQUE DE CAYLEY
SEXTIQUE RATIONNELLE
SICI (SPIRALE)
SIGMOÏDE
SIMPLE (COURBE)
SINUSOÏDAL (COURBE
A RAYON /)
SINUSOÏDALE
(SPIRALE/)
SINUSOÏDE
SINUSOÏDE DE BÉLIDOR
SINUSOÏDE
CIRCULAIRE
SINUSOÏDE
HYPERBOLIQUE
SLUZE (CUBIQUE DE/)
SLUZE (PERLE DE) loria p. 376
SOMMET
D'UNE COURBE
SPIRAL (COURBE DU RESSORT/)
SPIRALE
SPIRALE ANALLAGMATIQUE
SPIRALE D'ARCHIMÈDE
SPIRALE DE CORNU
SPIRALE DU COSINUS HYPERBOLIQUE
SPIRALE DE COTES
SPIRALE DE FERMAT
SPIRALE DE FIBONACCI
SPIRALE HYPERBOLIQUE
SPIRALE LOGARITHMIQUE
SPIRALE DE NORWICH
SPIRALE D'OR
SPIRALE A QUATRE (n)
CENTRES
SPIRALE SICI
SPIRALE DU SINUS HYPERBOLIQUE
SPIRALE SINUSOÏDALE
SPIRALE DE STURM
SPIRALE
DE LA TANGENTE HYPERBOLIQUE
SPIRALE TRACTRICE
SPIRALE DE LA TIGE EN ROTATION
SPIRE CIRCULAIRE
(LIGNE DE CHAMP MAGNÉTIQUE INDUIT PAR UNE/)
SPIRIQUE PLANE
SPIRIQUE DE PERSÉE
SPLINE
SQUELETTE
STELLOÏDE
STEINER (HYPOCYCLOÏDE DE/)
STÉRÉOGRAPHIQUE
(PROJECTION/) D’UNE COURBE SPHÉRIQUE
STROPHOÏDALE (COURBE/)
STROPHOÏDE
STROPHOÏDE DROITE
ou STROPHOÏDE DE NEWTON
STURM (ROULETTE DE/)
STURM (SPIRALE DE/
SUPER-ELLIPSE
SUPERPOSITION
SVASTIKA
SYMÉTRIE DE ROTATION (COURBE
À/)
SYMÉTRIQUE D'UNE COURBE
PAR RAPPORT À UNE AUTRE
SYNCHRONE (COURBE/)
SYNODALES (COURBES/)
SYNTRACTRICE
SYNTRÉPENTES (COURBES/)
TABLEAU DE FIL (COURBE DE/)
TANGENTE
HYPERBOLIQUE (SPIRALE DE LA/)
TANGENTOÏDE
HYPERBOLIQUE
TALBOT (COURBE DE/)
TANGENTOÏDE
TASSE DE CAFÉ (COURBE DE
LA/)
TAUTOCHRONE
TÉTRACUSPIDE
TIGE EN ROTATION (SPIRALE DE
LA/)
TN (COURBE A DISTANCE/ CONSTANTE)
TOROÏDE
TOURNESOL
TORPILLE
TRACTOIRE
TRACTOIRE DE CERCLE
TRACTRICE
TRAJECTOIRE ORTHOGONALE
TRANSCENDANTE (COURBE/)
TRANSFORMATION DE BROCARD
TRANSFORMATION DE NEWTON
TRÈFLE À QUATRE FEUILLES
TRÈFLE ÉQUILATÈRE
TRICIRCULAIRE (COURBE/)
TRICUSPIDE
TRIDENT DE NEWTON
TRIELLIPSE
TRIFOLIUM
TRIFOLIUM DE CRAMER
TRIFOLIUM PARABOLIQUE
TRIFOLIUM RÉGULIER
TRISECTRICE
TRISECTRICE DE
CEVA
TRISECTRICE DE DELANGES
TRISECTRICE DE
LONGCHAMPS
TRISECTRICE DE MACLAURIN
TROCHOÏDALE (COURBE/)
TROCHOÏDE
TROCHOÏDE À
CENTRE
TROCHOÏDE À
BASE QUELCONQUE
TROIS-BARRES (COURBE DU/)
TROTT (QUARTIQUE
DE/)
TSCHIRNHAUSEN (CUBIQUE
DE/)
UNICURSALE (COURBE/)
VAN REES (FOCALE
DE/)
VASQUE
VÉLAIRE
VERSIERA
VISIERA
WATT (COURBE DE/)
WEIERSTRASS (COURBE
DE/)
WONDERGRAF
(COURBE DU/)
YING ET YANG
ZAHRADNIK
(CISSOÏDALE DE/)
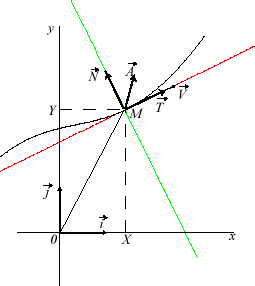
NOTATIONS
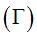 : courbe en cours d’étude.
: courbe en cours d’étude.
M : point courant de la courbe 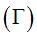 . .
(D) : droite, (C) : cercle.
(O, 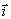 , , 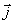 )
: repère orthonormé direct, d’axes Ox et Oy. )
: repère orthonormé direct, d’axes Ox et Oy.
(x, y) : coordonnées cartésiennes
de
M.
X et Y : projetés de M sur
Ox
et
Oy.
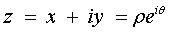 affixe de M.
affixe de M.
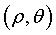 :
coordonnées polaires de M ; :
coordonnées polaires de M ; 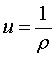 . .
t : paramètre (temps).
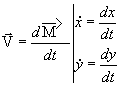 ,
vecteur vitesse. ,
vecteur vitesse.
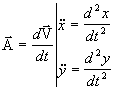 ,
vecteur accélération. ,
vecteur accélération.
Pour une courbe implicite 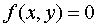 ,
notations de Monge : ,
notations de Monge :
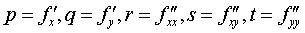 . .
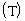 : tangente. : tangente.
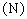 : normale.
: normale.
s : abscisse curviligne
(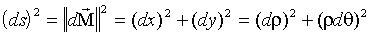 , ,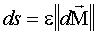 ) )
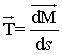 : vecteur tangent.
: vecteur tangent.
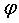 :
mesure de l'angle tangentiel cartésien :
mesure de l'angle tangentiel cartésien 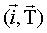 ,
défini par ,
défini par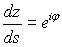 , soit
, soit 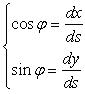 ,
d'où ,
d'où 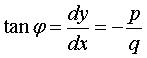 . .
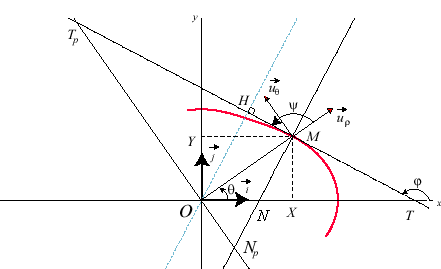
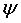 :
mesure de l'angle tangentiel polaire :
mesure de l'angle tangentiel polaire 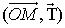 , défini par
, défini par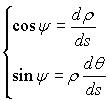 ,
d'où ,
d'où 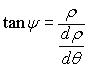 ; de plus
; de plus 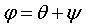 . .
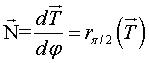 : vecteur normal.
: vecteur normal.
| Coordonnées de |
dans la base 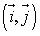 |
dans la base 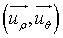 |
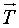
|
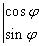
|
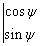
|
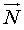
|
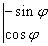
|
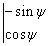
|
V : vitesse (algébrique) (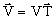 ). ).
AT
: accélération tangentielle, AN
: accélération normale (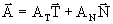 ). ). |

 |

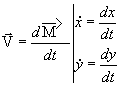 ,
vecteur vitesse.
,
vecteur vitesse.
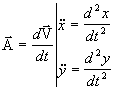 ,
vecteur accélération.
,
vecteur accélération.




