Les courbes étudiées sur cette page sont les courbes dont le rayon de courbure est une fonction sinusoïdale de l'abscisse curviligne.
 

Équation intrinsèque 1 : . Équation intrinsèque 2  pour 0  < 1 :  Paramétrisation cartésienne : avec  ; en complexes : . Équation intrinsèque 2  pour  = 1 :  Paramétrisation cartésienne : avec  ; en complexes : . Équation intrinsèque 2  pour  > 1 : . Paramétrisation cartésienne :  avec ,  ; en complexes : . Courbe transcendante.

 

Evolution d'une portion de courbe entre deux points à courbure infinie, pour lambda compris entre 0 et 1.	courbe pour lambda = 1	courbe pour n =1 (soit  lambda = rac(2))
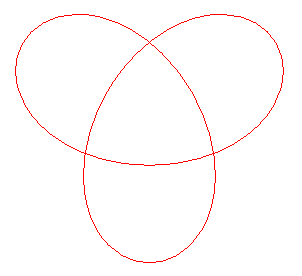
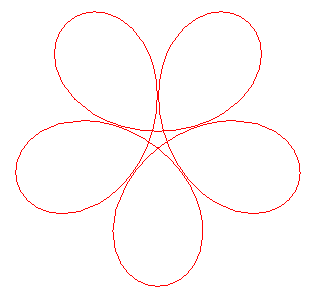
courbe pour n =3/2 (soit lambda = rac(13/9))	courbe pour n =2 (soit lambda = rac(5))	courbe pour n =3 (soit lambda = rac(10))

 
 

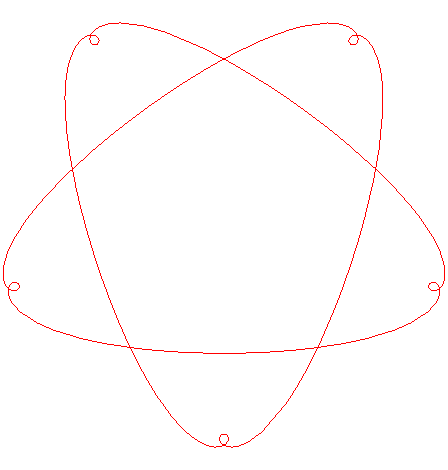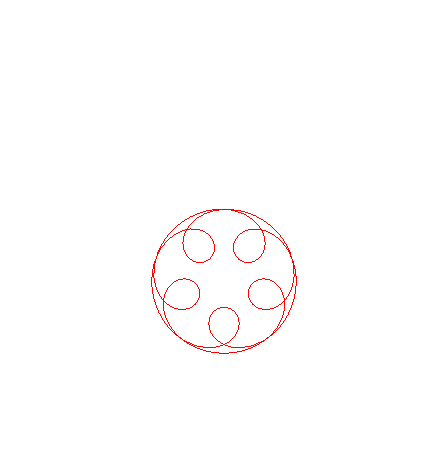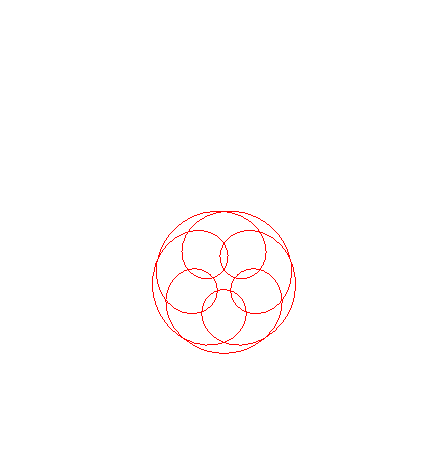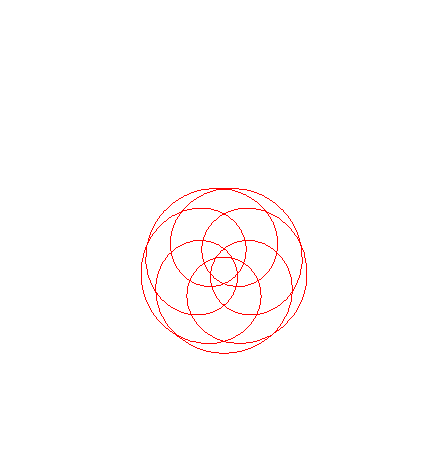
Si l'on désolidarise les valeurs de n et lambda dans , on obtient des courbes assez esthétiques rappelant dans certains cas les hypotrochoïdes. Si n est un rationnel, ce sont des courbes de Goursat d'ordre le numérateur de n. Ci-contre dans les cas n = 5/7, pour des valeurs de lambda croissant à partir de 1,01.

 

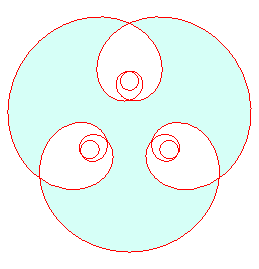
En faisant cette fois varier l'amplitude de la sinusoïde, on peut aussi considérer la famille des courbes d'équation intrinsèque 1 : ,  ayant pour paramétrisation :  Ci-contre une animation pour k allant de 0 à 3, avec arrêts à k =1 correspondant au cas =0 ci-dessus.

Les courbes dont la courbure varie sinusoïdalement avec l'abscisse curviligne sont les courbes des méandres.

Autres courbes définies par leur équation intrinsèque : la clothoïde, la courbe de giration constante, la courbe des forçats.

© Robert FERRÉOL 2011