Courbe des méandres

COURBE DES MÉANDRES
Meander curve, Mäanderkurve

Courbe étudiée par A.A. Savelov en 1960 (voir [Savelov] p. 264,265, lire en ligne], Luna Léopold et Walter Langbein en 1966 (cf. cet article), à laquelle ils ont donné le nom de sine-generated curve.
On retrouve cette courbe sous le nom de patterned curve, dans cette étude de Rovenski.

Équation intrinsèque 2 :

.
Équation intrinsèque 1 :

.
Paramétrisation cartésienne :

(

) ; en complexes :

.
Courbe transcendante.
Remarque : la courbe de paramétrisation

est semblable à la précédente.

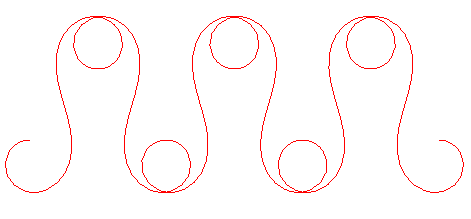
La courbe des méandres est la courbe telle que l'angle de la tangente avec une direction fixe varie sinusoïdalement avec l'abscisse curviligne. Une telle courbe a été envisagée par Luna Léopold car il avait constaté expérimentalement que l'aiguille d'une boussole dans un bateau descendant à vitesse constante une rivière à méandres oscillait de façon sinusoïdale au cours du temps.
Vu l'équation intrinsèque 1 ci-dessus, la courbe des méandres est aussi la courbes dont la courbure varie sinusoïdalement avec l'abscisse curviligne.

La courbe des méandres est aussi la courbe décrite par un point M tel que si une droite (D) fait un angle avec la tangente en M proportionnel à l'abscisse curviligne, le projeté H du centre de courbure I sur (D) est à distance constante non nulle de M.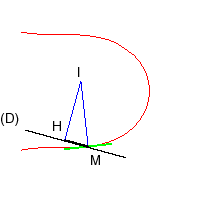

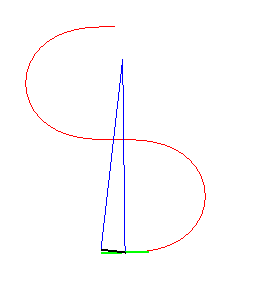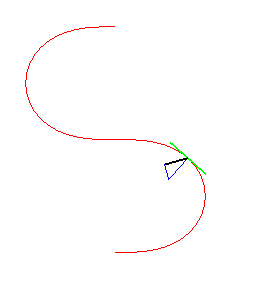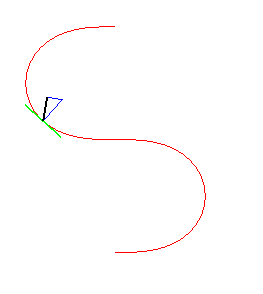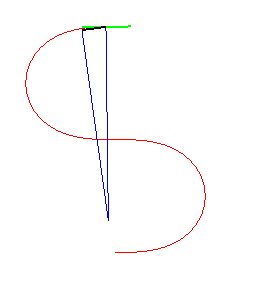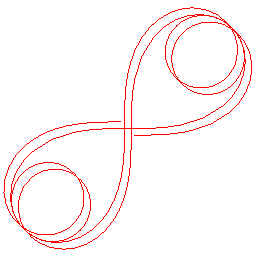
Voici l'évolution de la courbe suivant les valeurs de l'angle tangentiel maximal :

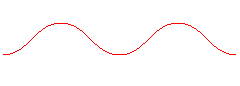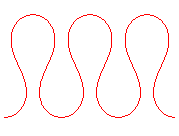
Pour inférieur à la courbe a une allure de sinusoïde ; ci-dessus, .

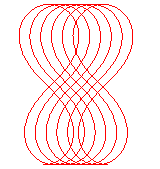
C'est pour que la courbe a le plus une allure de méandres.

Allure pour ,
plus précisément pour

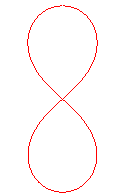
Pour , la courbe a une forme de lemniscate

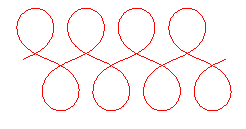
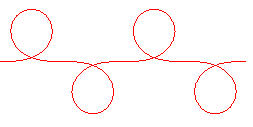
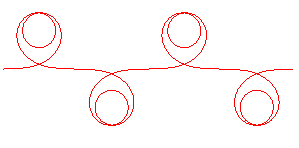
REM : les valeurs de donnnant une courbe bornées sont définies par (qui implique ).

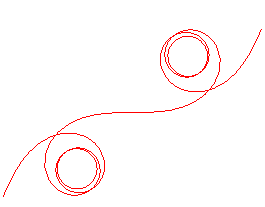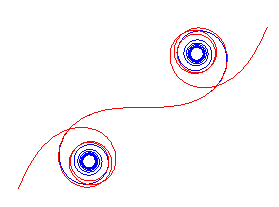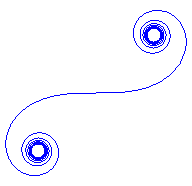Lorsque tend vers l'infini, la courbe des méandres : (en rouge) "tend" vers la clothoïde : (en bleu), ici pour = 10 :

Inversement, pour des petites valeurs de la courbe des méandres est très proche de la courbe élastique (et l'explication en est donnée sur la page correspondante) ; en fait, l'interprétation des méandres comme courbe minimisant la courbure conduit à modéliser les méandres plutôt par la courbe élastique, mais l'assimilation entre les deux courbes montre que Luna Léopold avait fait une bonne observation expérimentale.

Comparer aussi avec la courbe de giration constante et les courbes à rayon sinusoïdal.

Les méandres de la Seine.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Pour inférieur à la courbe a une allure de sinusoïde ; ci-dessus, .		C'est pour que la courbe a le plus une allure de méandres.
Allure pour , plus précisément pour	Pour , la courbe a une forme de lemniscate