-1< k < 0 : pseudo-sinusoïde

k = 0  lintéaire droite

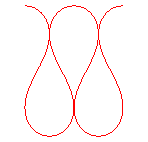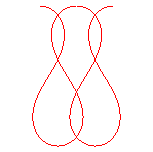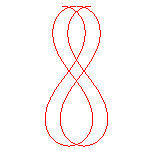
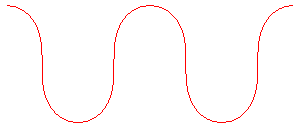
. 0<  k < k1 = 0.65222....

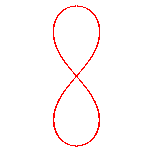
k = k1 = 0.65222.... : pseudo-lemniscate

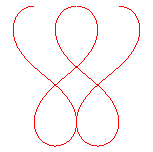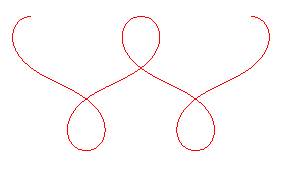
k1< k < -1

k = 1 : courbe des forçats

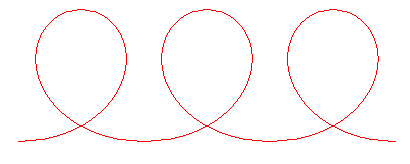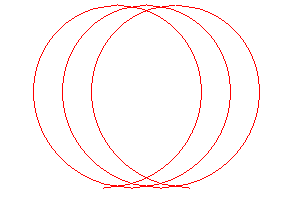
k > 1 : pseudo-trochoïde

Courbe étudiée par Jacques Bernoulli en 1691 qui lui a donné le nom d'elastica, par Euler en 1744, et Poisson en 1833. Autres nom : lintéaire, radioïde aux abscisses. Voir sur cette page d'Alain Esculier un programme de tracé de cette courbe.

Les courbes élastiques sont les courbes planes dont la courbure en tout point est proportionnelle à la distance à une droite fixe, appelée la directrice.
 

Prenant comme directrice l'axe des y, la condition s'écrit  (1) , d'où l' Équation différentielle : . (1) s'intègre en soit .  Posant, on obtient la paramétrisation : () Abscisse curviligne : , ou  ; rayon de courbure : .

Pour –1 < k < 1  (figure avec k = 1/ 2  : angle tangentiel à l'origine de - 30 °)

Si on utilise la paramétrisation :	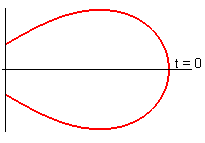Si on utilise l'expression explicite :
Paramétrisation cartésienne :  Posant , on obtient la courbe complète par , avec q entier.	Ici,  où   est l'angle tangentiel à l'origine. Équation cartésienne : où  ;  posant , on obtient la courbe complète par , avec q entier.

Pour k = 1 :

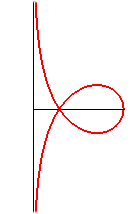L'intégrale n'est plus elliptique et on a la paramétrisation : () qui n'est autre que celle de la courbe des forçats, cas particulier de syntractrice.

Pour k > 1 :

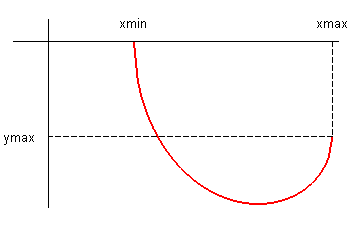Équation cartésienne :  avec  et  ; posant , on prolonge la courbe en  , avec q entier.

D'après la loi de Laplace le profil d'une bâche rectangulaire remplie d'eau est une courbe élastique (la courbure de cette bâche devant être proportionnelle à la distance à la surface du liquide), d'où le nom de lintéaire.
On retrouve la courbe élastique comme trajectoire d'une torpille dont le gouvernail tourne d'un angle proportionnel à la profondeur.

Mais la courbe élastique est aussi la solution du problème de calcul des variations suivant : trouver parmi toutes les courbes de longueur donnée celle qui minimise l'intégrale du carré de la courbure  ; autrement dit, c'est la courbe minimisant la variance des oscillations de la tangente par rapport à une direction fixe. C'est la raison pour laquelle on la retrouve dans de nombreux phénomènes naturels.
 

Une lame élastique contrainte prend une forme de courbe élastique (d'où le nom)	Lors de cet accident ferroviaire, les rails transportés ont pris une forme de courbe élastique, appelée par les physiciens "serpentin de flambage"	Les ondulations du serpent, minimisant la courbure, ont des formes de courbe élastique.

Les méandres des rivières prennent des formes de courbe élastique (voir aussi la courbe des méandres) Ici, les méandres de la Somme.

Sa propriété caractéristique de minimisation de la courbure fait que la courbe élastique est parfois utilisée dans les tracés de routes entre deux portions rectilignes, d'où son nom de radioïde aux abscisses.

Elle est aussi solution de cet autre problème de calcul des variations : trouver une courbe de longueur donnée joignant deux points donnés A et B, dont la rotation autour d'une droite (D) coplanaire avec la droite (AB) engendre un solide de volume maximal (autrement dit,  maximal, à  constant).

Et elle est aussi caractérisée par le fait que lorsqu'un point M la décrit à vitesse constante, la tangente oscille autour de M comme un pendule simple oscillerait autour de la parallèle à la directrice passant par M. (cf. la formule ).

C'est la raison pour laquelle la courbe élastique est très similaire, pour les valeurs de k comprises entre –1 et 1 à la courbe des méandres (dont la tangente oscille, elle, de manière sinusoïdale), et qu'elle est souvent confondue avec cette dernière.

Voir sur ce site allemand une très belle animation d'une généralisation de cette courbe.

Voir aussi la goutte d'eau pendante, généralisation à l'espace de la courbe élastique.

Les courbes telle que la courbure est proportionnelle à la distance à un point fixe (au lieu d'une droite) sont étudiées sur la page des spirales de Norwich ; on trouve en particulier la lemniscate de Bernoulli.
Les courbes telles que la courbure est proportionnelle à l'abscisse curviligne sont les clothoïdes.
Les courbes telles que la courbure est proportionnelle à la distance au point d'intersection de la normale avec une droite fixe sont étudiées ici.

REM : si dans l'équation différentielle  on remplace l'exposant 3/2 par 1/2, on obtient la courbe de la corde à sauter.

© Robert FERRÉOL  2010