La lintéaire est la forme prise par le profil d'une bâche rectangulaire attachée à deux barres horizontales, remplie d'eau jusqu'aux deux barres (deux plans limitant l'écoulement de l'eau) et placée dans un champ de pesanteur uniforme ; la bâche est supposée flexible, infiniment mince, inextensible et sans masse propre.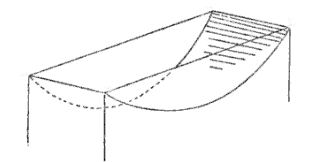

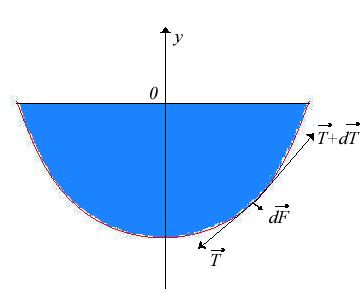
Avec les notations de la figure ci-dessus ( = tension transversale de la bâche en M), écrivons que la somme des forces en M est nulle :  où , ce qui exprime que la force de pression est proportionnelle à la profondeur y et à l'élément de longueur ds, et qu'elle est dirigée perpendiculairement au profil de la bâche.

Ceci se simplifie en , qui, par intégration, donne .

On en déduit 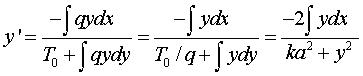, d'où, en éliminant l'intégrale, l'équation différentielle de la lintéaire : .
En posant , on obtient la paramétrisation : , pour , qui n'est autre que celle de la courbe élastique (échanger x et y).

La lintéaire est donc aussi la courbe dont la courbure est proportionnelle à la profondeur, ce qui pouvait s'obtenir directement en utilisant la loi de Laplace.

Remarque : pour une force de pression qui serait toujours proportionnelle à la profondeur y mais aussi à l'élément de longueur dx au lieu de ds, et dirigée vers le bas, soit , on obtiendrait une sinusoïde.

Voir la goutte pendante, généralisation à l'espace de la lintéaire.

Comparer avec la courbe de la corde à sauter.

© Robert FERRÉOL  2007