La courbe de la corde à sauter est la forme prise par un fil pesant flexible homogène inextensible en rotation autour d'un axe accroché à deux points de cet axe (en négligeant la pesanteur) ; impossible de la différentier à l'oeil nu d'une arche de sinusoïde, et pourtant c'est la représentation graphique de la fonction elliptique de Jacobi notée sn, et non celle de la fonction sinus.

On montre que la courbe de la corde à sauter d'extrémité A et B de longueur L est aussi la courbe de longueur L joignant A à B ayant le plus grand moment d'inertie par rapport à l'axe (AB).
 

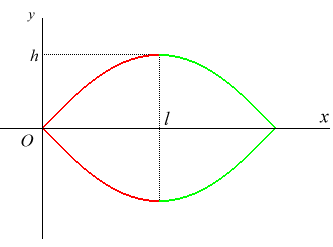Équation différentielle :  . Équation cartésienne : . Paramétrisation cartésienne exprimée avec la fonction elliptique de première espèce F (EllipticF en Maple) :  avec  ; Équation cartésienne exprimée avec la fonction elliptique de Jacobi sn (JacobiSN en Maple) : . Pente en O :  ;  Abscisse des sommets : . Longueur d'une arche : .

 

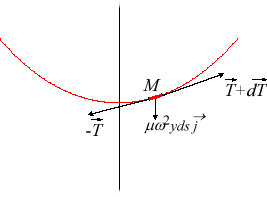Avec les notations de la figure ci-contre ( = tension du fil en M,  = masse linéique du fil,  = vitesse angulaire de rotation) , écrivons que la somme des forces en M est nulle : . Ceci se simplifie en , qui par intégration donne . D'où  et  soit  avec . Cette équation du deuxième ordre donne l'équation du premier ordre ci-dessus.

Si dans l'équation  on remplace l'exposant 1/2 par 3/2, on obtient la lintéaire.
Pour une autre courbe représentation d'une fonction elliptique de Jacobi, voir à couple roue-route.

© Robert FERRÉOL, Jacques MANDONNET 2008