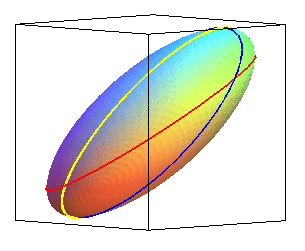
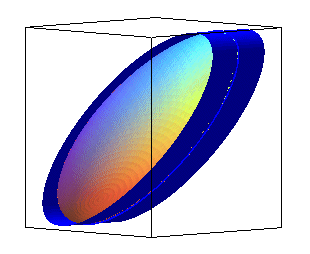
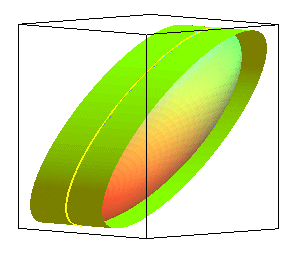
Vue d'un ellipsoïde et de 3 de ses contours apparents,  pour des observateurs situés à l'infini, suivant Ox, Oy, Oz et les cylindres de contact correspondants.

 

Une direction D étant choisie, on appelle contour apparent d'une surface (S), dans cette direction et pour un observateur à l'infini, le lieu des projetés sur un plan P perpendiculaire à D des points de la surface pour lesquels le plan tangent est parallèle à D. Le contour apparent est donc aussi :     - l'intersection avec P du cylindre de contact de la surface dans la direction D, formé des droites parallèles à D et tangentes à (S).     - l'enveloppe des sections avec P des plans tangents parallèles à D     - l'enveloppe des projections sur P des courbes de niveau de la surface associées à la direction D     - plus généralement, l'enveloppe des projetés sur P de toute famille de courbes engendrant la surface. Certains auteurs désignent par contour apparent le lieu sur la surface des points à plan tangent parallèle à D ; nous le désignerons par contour apparent réel (ou à la source), l'autre étant alors dit projeté.

Une direction D étant choisie, on appelle contour apparent d'une surface (S), dans cette direction et pour un observateur placé en A, le lieu des projetés de sommet A sur un plan P perpendiculaire à D et ne passant pas par A des points de la surface pour lesquels le plan tangent passe par A. Le contour apparent est donc aussi :     - l'intersection avec P du cône de contact de la surface de sommet A, formé des droites passant par A et tangentes à (S).     - l'enveloppe des sections avec P des plans tangents passant par A     - l'enveloppe des projetés coniques de centre A sur P de toute famille de courbes engendrant la surface. Remarquons que le contour apparent reste semblable à lui même lorsque le plan P varie. Certains auteurs désignent par contour apparent le lieu sur la surface des points à plan tangent passant par A ; nous le désignerons par contour apparent réel (ou à la source), l'autre étant alors dit projeté.

 

Contour apparent dans la direction de Oz et pour un observateur placé à l'infini : si la surface est définie par l'équation cartésienne (1) : f(x,y,z)=0, l'équation du  contour s'obtient en éliminant z entre (1), et (2) : . Si elle est définie paramétriquement par (M(u,v)), on obtient v = v(u) en écrivant  et la paramétrisation du contour apparent est x = x(u,v(u)), y = y(u,v(u)).

Contour apparent dans la direction de Oz et pour un observateur placé en A(0,0,a) : si la surface est définie par l'équation cartésienne (1) : f(X,Y,Z)=0, l'équation du contour dans le plan xOy s'obtient en éliminant X,Y, et Z entre (1), (2) :  et (3) : . Si elle est définie paramétriquement par (M(u,v)), on obtient v = v(u) en écrivant , et la paramétrisation du contour apparent est x = x(u,v(u)), y = y(u,v(u)).

Exemples :

    - les contours apparents d'une sphère sont des cercles (et réciproquement, une surface dont tous les contours apparents pour des observateurs à l'infini sont circulaires est une sphère).
    - les contours apparents (réels ou projetés, à distance finie ou non) d'une quadrique sont des coniques (ils sont donc plans)
    - les contours apparents d'une surface algébrique de degré n sont des courbes algébriques de degré n(n – 1) (?).
    - le contour apparent projeté d'un tube est formé de deux courbes parallèles à la projection sur xOy de la courbe centrale ; en particulier les contours apparents du tore sont les courbes parallèles à l'ellipse, d'où leur nom de toroïdes.
    - le cylindre de contact dans la direction de D (resp. de sommet A) d'une surface développable est formé des plans tangents à la surface qui sont parallèles à D (resp. passant par A) ; le contour apparent réel est formé des directrices dont le plan tangent est parallèle à D (resp. passe par A) , et le contour apparent projeté est formé de droites (deux droites pour un cône ou un cylindre de révolution).
 
 
 

Ci-contre, vue d'une surface avec ses contours apparents pour un observateur situé à distance finie, le réel en bleu et le projeté en noir, avec à droite le cône de contact.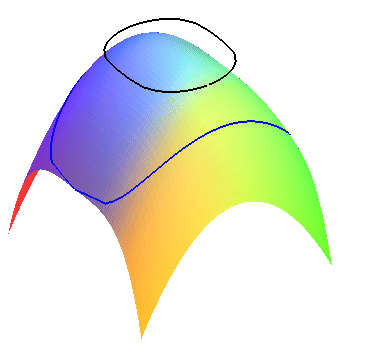

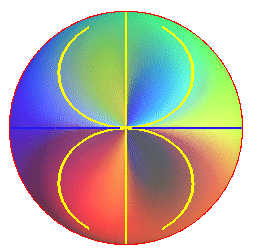
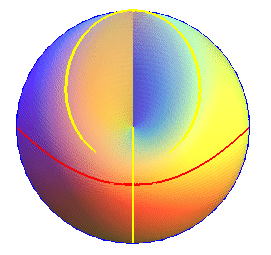
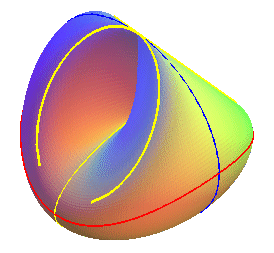
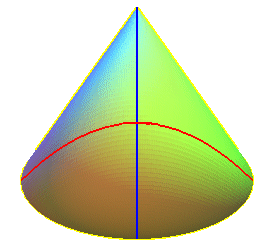
Ci-dessous des vues du bonnet croisé avec 3 contours apparents pour des observateurs situés à l'infini, suivant Oz (en rouge), suivant Ox (en bleu) et suivant Oy (en jaune).
 
 

L'intersection de 3 cylindres d'axes perpendicualires a trois contours apparents à l'infini suivant ces 3 axes qui sont des cercles de mêmes rayons, mais n'est pas une sphère. Image : Alain Esculier.

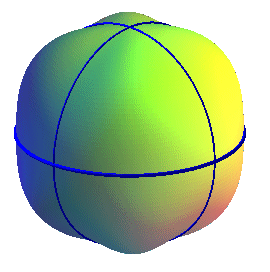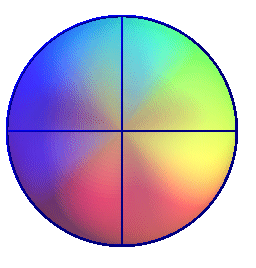Cette sphère boursoufflée, d'équation sphérique  possède la même propriété, tout en ayant un plan tangent en tout point.

On définit en topologie une notion voisine : le contour apparent d'une partie X de l'espace est la frontière du projeté de X sur un plan P, projeté orthogonal pour un observateur à l'infini, projeté de centre A pour un observateur en A. Les deux notions coïncident par exemple si X est une surface de classe C¹,  frontière d'un convexe de l'espace.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2019