Quadrique

QUADRIQUE
Quadric, Quadrik

Du latin quadrus : carré.

Une quadrique est une surface algébrique de degré 2 ; voir la classification ci-dessous.

Équation cartésienne : , où P est un polynôme du second degré.
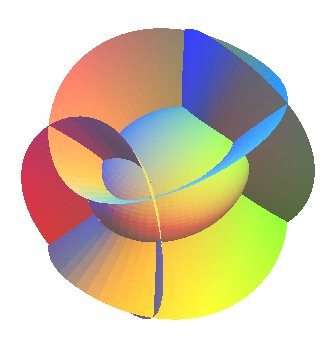
La quadrique est dite propre si la forme quadratique homogène est non dégénérée, c'est-à-dire de rang 4 (ce qui revient à dire que la surface est lisse).
Lorsque le rang de cette forme vaut 3, on obtient les cônes et cylindres du second degré et lorsqu'il est inférieur ou égal à 2, la quadrique est décomposée en réunion de deux plans.
Équation cartésienne réduite (à isométrie près) des quadriques : avec .
I) Classification affine réelle.
A transformation affine près, Il y a 9 cas réels, non vides, non décomposés et non réduits à un point, 5 propres et 4 de rang 3 :
1) Les trois non nuls de mêmes signes : ellipsoïde d'équation réduite .
2), 3) et 4) Les trois non nuls et non de mêmes signes : hyperboloïde à une nappe, à deux nappes ou cône elliptique (de rang 3) d'équations réduites respectives .
5), 6) L'un des nul, les deux autres de mêmes signes : paraboloïde elliptique : ou cylindre elliptique (de rang 3) : .
7), 8) L'un des nul, les deux autres de signes contraires : paraboloïde hyperbolique : ou cylindre hyperbolique (de rang 3) : .
9) Deux des nuls, l'autre non : cylindre parabolique (de rang 3) : .
II) Classification projective réelle.
Il n'y a plus que 2 types propres non vides :

ellipsoïde,
paraboloïde elliptique,
hyperboloïde à 2 nappes :
quadriques propres à points elliptiques

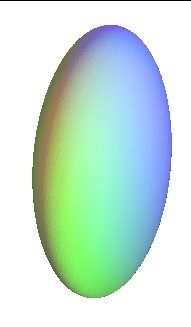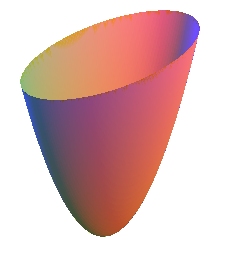
A homographie près, ces 3 quadriques sont identiques !

et
hyperboloïde à une nappe
paraboloïde hyperbolique :
quadriques propres réglées (à points hyperboliques)

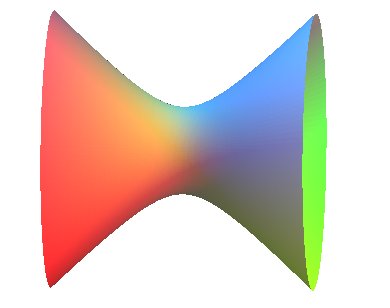
Idem pour celles-ci.

et un type non vide de rang 3 : .
III) Classification projective complexe :
Un type propre : et un type de rang 3 : .

Quadriques homofocales et système triple orthogonal de quadriques propres.
Si a > b > c, les quadriques d'équation sont des quadriques propres dont les sections par les plans de symétries sont des coniques confocales (i.e. de même foyer) ; les 6 foyers sont , , .
Pour on obtient une première famille, formée d'ellipsoïdes, pour on obtient une deuxième famille, formée d'hyperboloïdes à une nappe, pour , une troisième famille, formée d'hyperboloïdes à deux nappes.
De plus ces trois familles forment un système triple orthogonal, ce qui signifie chaque surface de chaque famille coupe orthogonalement chaque surface des deux autres familles.
Les lignes d'intersection sont des lignes de courbure (théorème de Dupin).
Ci-contre, un exemple de chaque famille ; pour savoir quel est l'hyperboloïde qui est à deux nappes, regardez : .

Contrairement au cas plan, l'équation , où F(a, 0,0) est un point et H le projeté de M sur une droite (D) = Oz, ne donne pas toutes les quadriques. L'équation réduite étant , on obtient un ellipsoïde de révolution pour k < 1, un cylindre parabolique pour k = 1, et un hyperboloïde de révolution pour k > 1 (ci-contre).

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres