Une surface est dite algébrique lorsqu’elle possède une équation cartésienne polynomiale à coefficients réels.

Le degré (ou parfois l'ordre) d'une surface algébrique d'équation 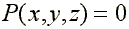 est le degré du polynôme P, supposé sans facteur carré ;
c'est aussi le nombre de points d'intersection, comptés avec les multiplicités, de la surface avec une droite quelconque, dans l'espace projectif complexe (et dans la pratique, le nombre maximum de points d'intersection de la surface avec une droite dans l'espace affine réel est un minorant du degré et donne très souvent le degré).
La notion de degré est projective, à savoir que toute homographie transforme une surface algébrique en une surface algébrique de même degré.
La surface est dite décomposable si elle est réunion de surfaces algébriques de degré plus petit et indécomposable dans le cas contraire, c'est-à-dire quand le polynôme P est irréductible dans .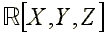

Les surfaces de degré 1 sont les plans, de degré 2 les quadriques, de degré 3 les surfaces cubiques, de degré 4 les surfaces quartiques.

Exemples de surfaces algébriques de degré 6, ou sextiques : les surfaces dodécaédriques de Goursat (dont la sextique de Barth), la surface du sinus, un tore sinusoïdal.

Exemple de surface algébrique de degré 8 : l'oloïde.

Exemple de surface algébrique de degré 9 : la surface d'Enneper.

Toute surface rationnelle est algébrique, mais la réciproque est fausse.
 
 

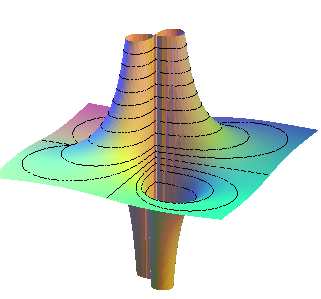
	Une jolie surface quintique, 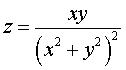, dont les sections horizontales sont des lemniscates de Bernoulli.
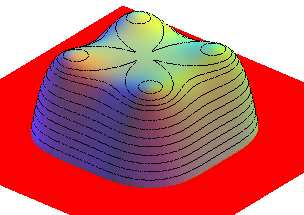
	La sextique 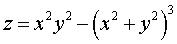 dont la courbe de niveau 0 est un quadrifolium.

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2005