1) Première espèce :
 

Paramétrisation cartésienne : , pour une surface tangente au tore classique de grand rayon a et de petit rayon b. Équation cylindrique pour k = 1/2 : . Équation cartésienne correspondante (surface algébrique du sixième degré) : a^4 y^2 - 2 a^2 b^2 y^2 + b^4 y^2 - 2 a^2 x^2 y^2 - 2 b^2 x^2 y^2 + x^4 y^2 - 2 a^2 y^4 - 2 b^2 y^4 + 2 x^2 y^4 + y^6 + 4 a^2 x^2 z^2 - 4 b^2 x^2 z^2 - 8 a x^3 z^2 + 4 x^4 z^2 + 4 a^2 y^2 z^2 - 4 b^2 y^2 z^2 - 8 a x y^2 z^2 + 8 x^2 y^2 z^2 + 4 y^4 z^2 + 4 x^2 z^4 + 4 y^2 z^4=0

Les tores sinusoïdaux de première espèce sont les surfaces engendrées par la rotation d'une ellipse variable autour d'un axe, l'ellipse située dans un plan perpendiculaire à l'axe, un axe de l'ellipse restant constant et l'autre variant sinusoïdalement.
 

On obtient une immersion 3D de la bouteille de Klein pour k = 1/2 et a > b > 0 ; les sommets principaux de l'ellipse génératrice décrivent deux cercles et les sommets secondaires une courbe de Viviani (en bleu ci-contre).
Ci-contre, le modèle réalisé en 1947 par Maurice El-Milick, conservé à l'IHP.	Photo : François Apéry
Dans le cas b = a, et toujours k = 1/2, la surface obtenue n'est autre, à dilatation près, que le bonnet croisé. La suppression du trou central a fait diminuer le genre de 1, donc passer de la bouteille de Klein au plan projectif.

 

Pour k quelconque, les sommets secondaire de l'ellipse décrivent une, ou deux, couronnes sinusoïdales de paramètre k.

Cas k = 1 : surface orientable la courbe bleue est une ellipse

Cas k = 3/2 : surface unilatère, immersion de la bouteille de Klein

Cas k = 2 : surface orientable ; la courbe bleue est une courbe de la crêpe

2) Deuxième espèce :
 

Paramétrisation cartésienne : , pour une surface tangente au tore classique de grand rayon a et de petit rayon b.

Les tores sinusoïdaux de deuxième espèce sont les surfaces engendrées par la rotation d'un cercle variable autour d'un axe, le cercle située dans un plan perpendiculaire à l'axe, le rayon du cercle variant sinusoïdalement ; autrement dit, c'est un tube d'âme un cercle de rayon variant sinusoïdalement.
 

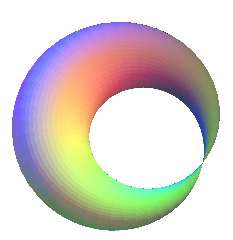
Pour k = 1/2, on obtient la surface à un point conique appelée "tore pincé". À ne pas confondre avec la cyclide de Dupin en croissant : (pour la première, la projection sur xOy est délimitée par un limaçon de Pascal à boucle, tandis que pour la seconde, elle est limitée par deux cercles tangents).

 

Quelques autres exemples :

Cas k = 1

Cas k = 2

Cas k = 3

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2013