Genre d'une surface

GENRE D'UNE SURFACE
Genus of a surface, Geschlecht einer Fläche

Notion étudiée par Abel, Jacobi, Riemann et Clebsch (qui a donné le nom).

Le genre d'une surface (i.e. un espace topologique dont tout point possède un voisinage homéomorphe au plan) connexe est le nombre maximum de courbes fermées simples sans points communs que l'on peut tracer à l'intérieur de cette surface sans la déconnecter (c'est-à dire que le complémentaire de ces courbes reste connexe) ; concrètement, si l'on considère que la surface est en papier, le genre est le nombre maximal de découpages fermés que l'on peut effectuer sans que la surface ne soit séparée en plusieurs morceaux.

Cette notion est topologique : deux surfaces n'ayant pas le même genre ne sont pas homéomorphes.

Par exemple, ceci permet de différencier
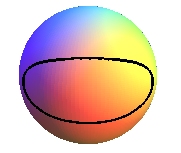
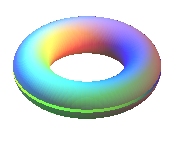
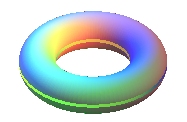
- la sphère, du tore :

la sphère est de genre 0 : toute courbe fermée simple la déconnecte, tandis que le tore T est de genre 1 : une courbe peut le laisser connexe, mais deux courbes sans point commun le déconnectent.

- le plan projectif, de la bouteille de Klein :

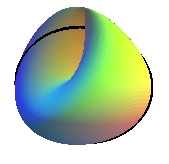
Le plan projectif réel P²(R) est de genre 1 (la courbe noire ci-dessus ne déconnecte pas le bonnet croisé, mais deux courbes, oui)
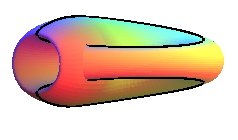
tandis que la bouteille de Klein K est de genre 2 (et non 1 comme on le voit parfois écrit) ; les deux courbes ci-dessus laissent la bouteille connexe.

Le genre caractérise les surfaces closes orientables, puisque le tore à n trous:T_n est de genre n, et il caractérise les surfaces closes non orientables, puisque la sphère munie de n bonnets croisés est de genre n.
Pour les surfaces closes, le genre est relié à la caractéristique d'Euler-Poincaré par les relations :
pour une surface orientable,
pour une surface non orientable.

Une surface close percée d'un nombre fini de trous (ouverts ou fermés, et homéomorphes à un disque) conserve son genre (alors que la caractéristique d'Euler-Poincaré est modifiée).

Exemples :
- le plan (sphère moins un point), le cylindre, avec ou sans bords (sphère percée de 2 trous), sont de genre nul.

- le ruban de Möbius ouvert ou fermé (plan projectif percé d'un trou) est de genre 1.

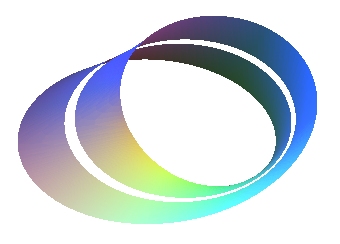
Découper un ruban de Möbius en son centre ne le déconnecte pas ; son genre est égal à 1.

- Le slip de Möbius (bouteille de Klein percée d'un trou) est de genre 2.

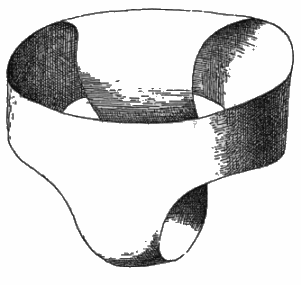
- Malgré ses 4 orifices, le rulpidon d'Ulysse Lacoste est de genre 3 :

les 3 courbes noires ne le déconnectent pas, une quatrième le ferait.

- Malgré ses 6 orifices, la première étape de l'éponge de Sierpinski est de genre 5 :

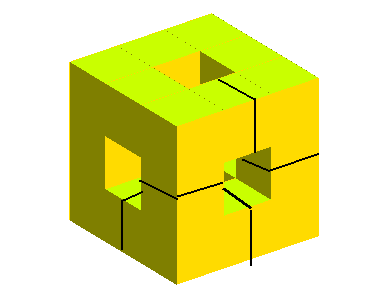
les 5 courbes noires ne la déconnectent pas ; une sixième le ferait.

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres