
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
GENUS OF A SURFACE
| Notion studied by Abel, Jacobi, Riemann and Clebsch (who named it). |
The genus of a connected surface (i.e. a connected topological space any point of which has a neighborhood homeomorphic to the plane) is the maximum number of simple closed curves without common points that can be traced inside this surface without rendering the resultant manifold disconnected (i.e. such that the complement of these curves remains connected); in concrete terms, if we consider that the surface is made of paper, then the genus is the maximum number of closed cuts that can be carried out without the surface being decomposed into several pieces.
This notion is topological: two surfaces with different genuses are not homeomorphic.
For example, this allows to distinguish
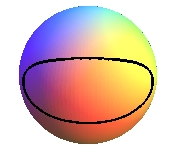
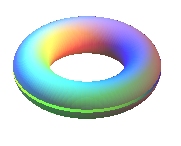
- the sphere from the torus:
  |
  |
- the projective plane from the Klein bottle:
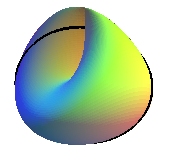
The real projective planeP2(R) is of genus 1 (the black curve above does not disconnect the cross-cap, but two curves do) |
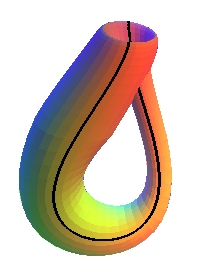
while the Klein bottle K is of genus 2 (and not 1 like it can sometimes be read); the two curves above leave the bottle connected. |
The genus characterizes the orientableclosed
surfaces, since the n-torus:Tn
is of genus n and characterizes the non-orientableclosed
surfaces, since the sphere with n cross-caps
is of genus n.
For the compact connected surfaces with no boundary,
the genus is related to the Euler
characteristic by the formulas:
for
an orientable surface,
for a non-orientable surface.
A closed surface in which have been drilled a finite number of holes (open or closed, and homeomorphic to the disk) keeps its genus (whereas the Euler characteristic is modified).
Examples:
- the plane (sphere minus a point),
the cylinder, with or without boundary (sphere with 2 holes), are of genus
zero.
- the open or closed Möbius strip (projective plane with one hole) is of genus 1.
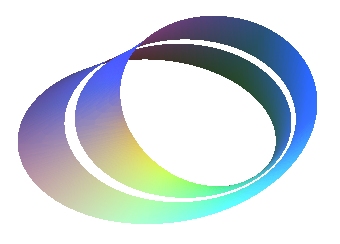
- The Möbius briefs (Klein bottle with one hole) is of genus 2.
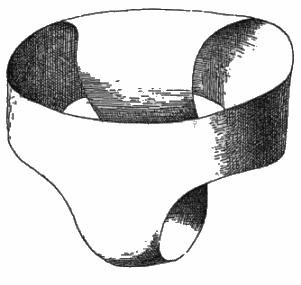

the 3 black curves do not disconnect it; a sixth would.
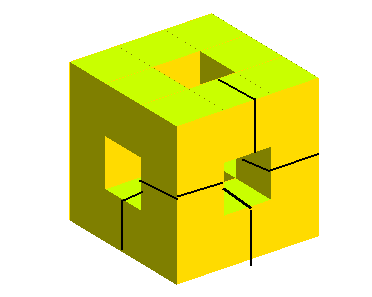
- The first step of Sierpinski's
fractal is of genus 5:
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2024