(REAL) PROJECTIVE PLANE
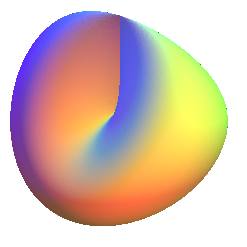

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
(REAL) PROJECTIVE PLANE

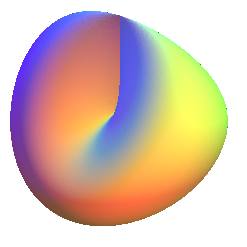

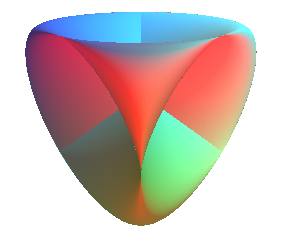
| Surface studied by Felix Klein in 1874. |
| Cartesian parametrization of an immersion in |
The (real) projective plane
is the quotient space of
by the collinearity relation.
But, more generally, the notion "projective plane" refers
to any topological space homeomorphic to .
It can be proved that a surface
is a projective plane iff it is a one-sided
(with one face) connected compact surface of genus
1 (can be cut without being split into two pieces).
| The chromatic
number of the projective plane is equal to 6 (any map traced on the
projective plane can be colored with no more than 6 colors, and there exist
maps that need 6 colors).
There even exist maps where each country touches the 5 others, one of which is represented opposite on the cross-cap, another one on a decagon with identified opposite sides with inversion of direction (cf. below). |
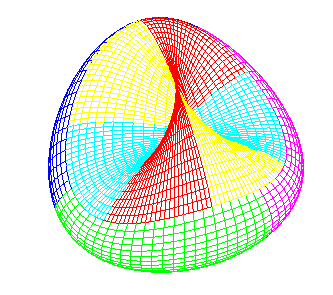 |
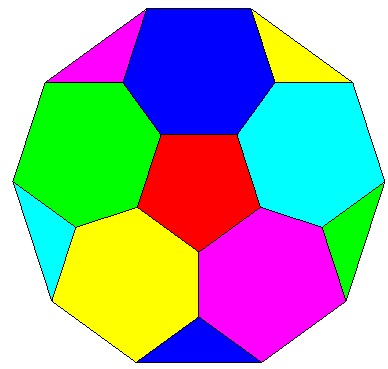 |
| The three
utilities problem can be solved on the projective plane, contrary to
the plane. In other words, the bipartite graph The same holds for the complete graph with 5 vertices |
 |
Here are classic models of the projective plane:
- The set of vectors of
with the natural topology
- A (real affine) plane completed
by a projective line (line at infinity)
- A sphere where the antipodal points
are identified
- A closed disk where the antipodal
points of the circumference are identified
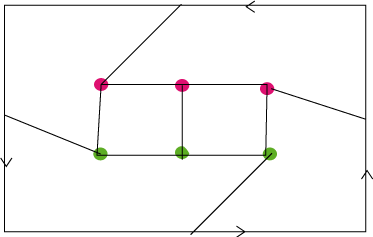
| - A closed disk two semi-circumferences of which are identified, with the indicated direction (amounts to the previous construction) | 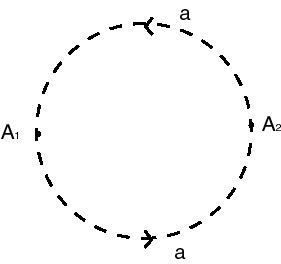 |
| - A full square the opposite sides of which
are identified with an inversion of direction.
This amounts to the previous construction, but allows to see the link with the Möbius strip in the following characterization (the strip being obtained by identification of only one pair of opposite sides). |
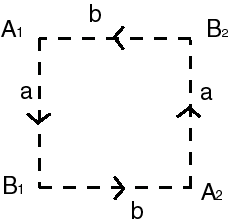 |
| - A Möbius strip the two half-edges of which are identified in opposite directions. (If they are identified in the same direction, we get a Klein bottle). |
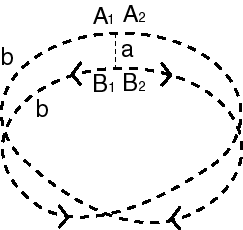 |
| - A Möbius
strip closed by a lid homeomorphic to a disk. A Möbius strip is
therefore a punctured projective plane.
To prove this start from the triangular representation of the Möbius strip and curb it. We can see the projective plane and its circular hole appear... |
|
- the star polyhedron with the same edges as the octahedron called tetrahemihexahedron.
The projective plane cannot be represented in
without self-intersection; the 4 classic immersions of the projective plane
in
are:
- the cross-cap
(the simplest)
- the Roman
surface (the first one that was historically discovered)
- Boy's
surface (more complex, but without "pinch
points", contrary to the first two)
- Henneberg's
minimal surface, which is, additionally, a minimal surface.
The equations given in the header are those of the surfaces
of obtained
by immersion of the projective plane.
For ,
we get the cross-cap,
for ,
the Roman surface,
and for ,
we get Boy's surface (equations of Apery).
The Veronese surface
is an embedding of the projective plane in .
Here are 2 constructions of the projective plane illustrated on the cross-cap.
 A Möbius strip (with self-intersection, but there is a boundary, a face) |
 + a disk (with self-intersection, but there is a boundary and two faces) |
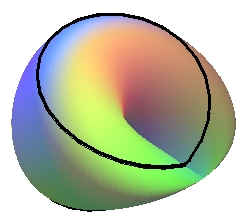
= a projective plane |
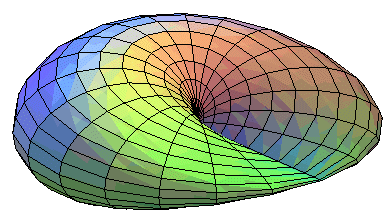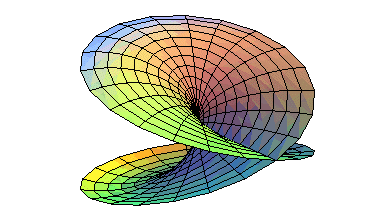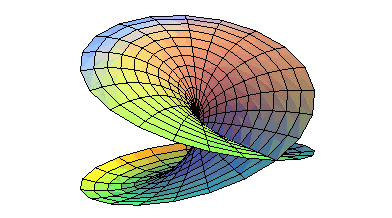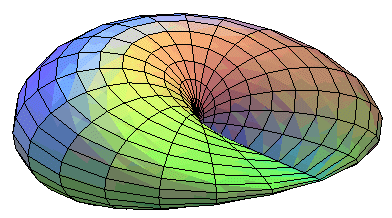
A disk can be deformed so that the points on two semi-circumferences come together: |

this... |

...is indeed equivalent to this! |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017