MÖBIUS STRIP


| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
MÖBIUS STRIP
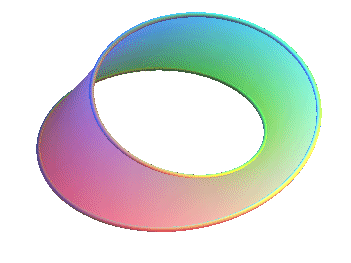


| Surface studied by Listing
and Möbius in 1858.
August Ferdinand Möbius (1790-1868): German astronomer and mathematician. Other name: Möbius (or Moebius) band, ring, belt. |
| Rotoidal representation: see
Möbius
surface.
Wunderlich representation: surface envelope of the rectifying planes (i.e. the rectifying developable) of the rational curve:
Representation on Plücker's conoid. Simple method for drawing a Möbius strip with a pencil
from a three-loop hypotrochoid:
|
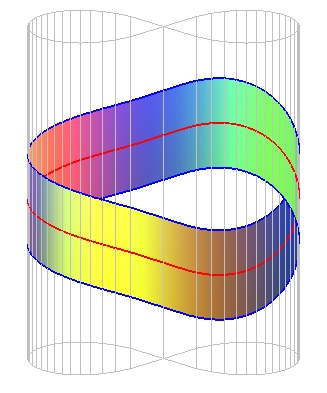
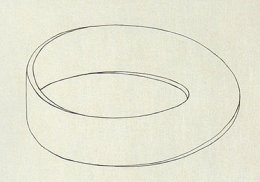
A Möbius strip is a surface obtained by sewing
together two sides of a rectangular strip with a half-twist, or any topologically
equivalent surface.
 |
Maple program giving an animation of the opposite construction.
with(plots):a:=1/2:b:=1/3:c:=1/6:d:=2/3:e:=1/3:C:=4/5: x0:=(1+d^2*t^2+2*d*e*t^4+e^2*t^6)/2:x:=(a*t+b*t^3+c*t^5)/x0:y:=(d*t+e*t^3)/x0: z:=-C/x0:t:=tan(tt): a1:=diff(v1,tt):a2:=diff(v2,tt):a3:=diff(v3,tt): v1:=diff(x,tt):v2:=diff(y,tt):v3:=diff(z,tt): b1:=v2*a3-a2*v3:b2:=a1*v3-v1*a3:b3:=v1*a2-a1*v2: n1:=simplify(v2*b3-b2*v3):n2:=simplify(b1*v3-v1*b3):n3:=simplify(v1*b2-b1*v2): dn1:=diff(n1,tt):dn2:=diff(n2,tt):dn3:=diff(n3,tt): c1:=n2*dn3-dn2*n3:c2:=dn1*n3-n1*dn3:c3:=n1*dn2-dn1*n2: facteur:=simplify(sqrt(b1^2+b2^2+b3^2)/(b1*c1+b2*c2+b3*c3)): c1:=simplify(c1*facteur):c2:=simplify(c2*facteur):c3:=simplify(c3*facteur): ds:=simplify(sqrt(v1^2+v2^2+v3^2)): s:=a->evalf(Int(ds,tt=0..a,4))/4: d:=a->plot3d([x/s(a)+u*c1/s(a),y/s(a)+u*c2/s(a),(z+2*C)/s(a)+u*c3/s(a)],tt=-a..a,u=-1/3*s(a)..1/3*s(a),grid=[150,2],style=patchnogrid): n:=40:display([seq(d(k*Pi/2.0001/n,50),k=1..n)],orientation=[-60,80],lightmodel=light2,insequence=true); |
Therefore, we obtain a Möbius strip by turning regularly
a segment of a line with constant length around a circle with a half-twist
or, more generally, an odd number of half-twits; these various strips are
homeomorphic,
but not isotopic in
(it is not possible to pass continuously from one surface to the other),
and for each number of half-twists, there exist two isotopy classes, mirror
images of one another:
| 1 half-twist | 3 half-twists | 9 half-twists | |
|
|
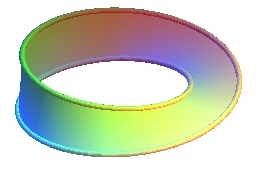 |
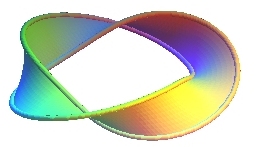 |
 |
|
|
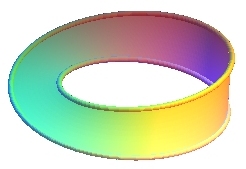 |
 |
 |
Moreover, the boundary of the strip with 3 half-twists
is a trefoil knot,
and, more generally,
the boundary of the strip with 2p + 1 half-twists is
a toroidal
knot of order (2p + 1, 2).
These rotoidal
surfaces are not developable:
they cannot be obtained from a piece of paper without tearing; inversely,
the strip that is naturally obtained with a rectangular piece of paper
does not have a simple parametrization; here is one owed to W. Wunderlich
(cf. above), in the right-handed case with one half-twist:
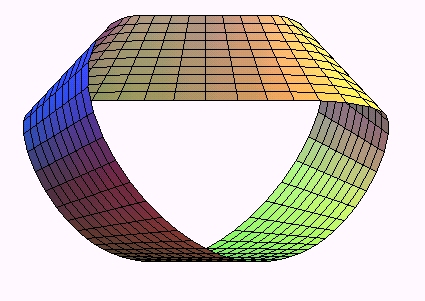 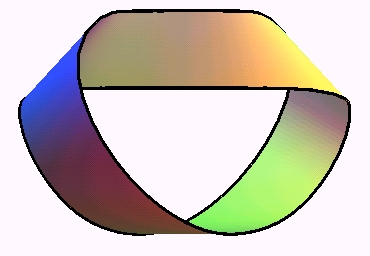 |
| The Möbius-Wunderlich strip has the property that it develops into a rectangle and it minimizes at all points the strain energy. |
Here is another example of a Möbius strip developable
into a rectangle, composed of 3 cylindrical sections joined by planar sections:
 |

Right-handed strip with 3 half-twists. |
Here are two other developable Möbius strips obtained
by putting strips cut on cones next to one another.
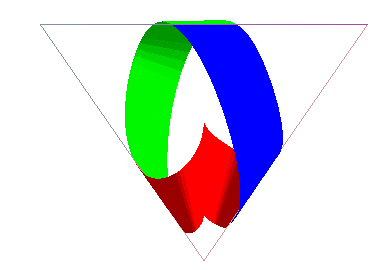 |
The blue and green strips are cut on cones of revolution; the red strip on two cones of revolution; the pattern is unfortunately not a rectangle, but a parallelogram, hence the connection with a right angle. |
 |
This is a Möbius strip with 3 half-twists instead
of 1, obtained thanks to 3 conical strips, the directrix of the cones being
Viviani's
curve.
The boundary is self-parallel, but the pattern does not have linear edges. |
 |
This strip with two half-twists (which is, therefore,
not a Möbius strip) is developable since it is traced on a cylinder
based on a lemniscate.
Its pattern does not have linear edges, but our eyes tend to think so,
hence our tendency to consider this figure to be impossible!
|
We can also wonder what ratios length/width of the initial
rectangle allow to construct a Möbius strip with no self-intersection:
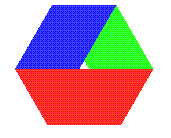
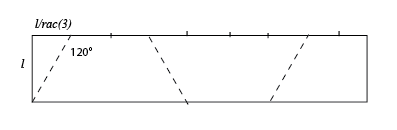
| Here is already a Möbius strip with one half-twist
for which the ratio length/width is equal to 3Ö3
(slightly greater in fact for the sake of clarity).
The view from above is a regular hexagon. The initial pattern is indicated on the right (the 3 folds are dotted). |
 |
 |
|
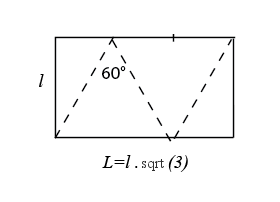
But with a rectangle for which the ratio length/width is equal to Ö3, you will construct a Möbius strip for which the view from above is an equilateral triangle. In 2023 it was proofed that we cannot do better than Ö3. |
 |
 |
 |
 |
 |
 |

The same one, tightened (almost) as much as possible: It cannot be tightened more without self-intersections. |

The same one, tightened (almost) as much as possible:
|

The same one, tightened (almost) as much as possible: |

The same one, tightened (almost) as much as possible:
|
| Therefore, except in the case n = 3, the Möbius
strip with n half-twists tightened as much as possible, with circumference
a regular n-gon, needs a rectangle |
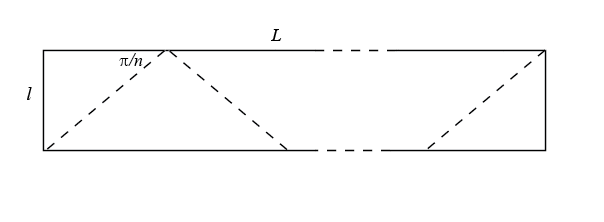 |
When a Möbius strip is cut at its center, we get
only one strip but with two edges, and 4 half-twists (and not 2 half-twists
like it could be believed); if it is cut at one third of its length, we
get a Möbius strip (at the center) and a strip with 2 entangled edges:
|
Strip with two half-twists, hence homeomorphic to the
cylinder, that provides a two-sheeted covering of the Möbius strip:
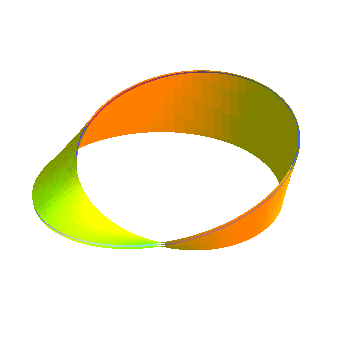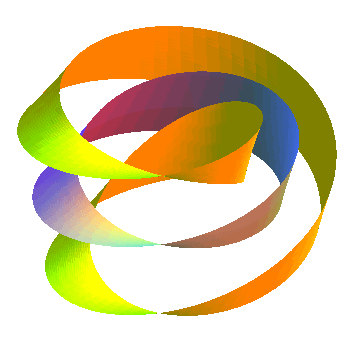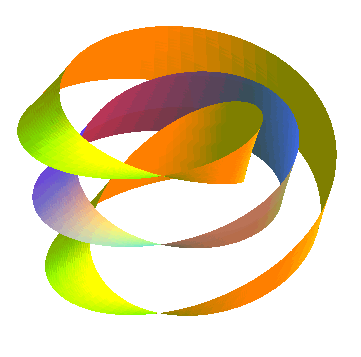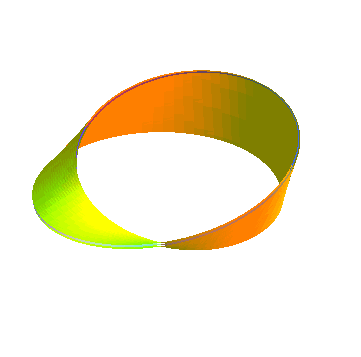 |
Just as the Klein bottle
cannot be represented in
without self-intersections, the Möbius strip cannot be represented
in the plane without self-intersections.
| The Möbius strip is a surface that can be characterized by the fact that it has only one face (in other words, it is one-sided, hence non-orientable), a unique boundary and its genus is equal to 1 (i.e. a closed curve traced inside it can leave it connected, but not two curves). | 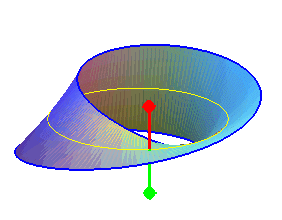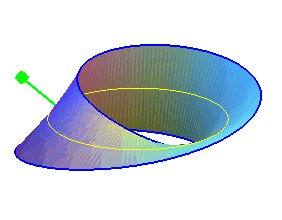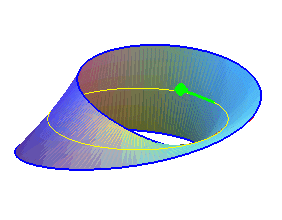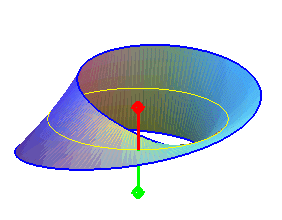 |
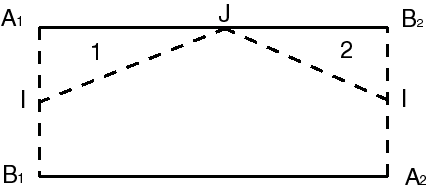
| We also get a topological Möbius strip by identification
of the opposite sides of a rectangle with an inversion of direction.
The oriented segment line [A1 B1] is identified to [A2 B2], so that there is only one boundary [A1 B2] linked to [A2 B1]. In the real strip, A1 = A2 =A and B1 = B2 = B. |
 |
| If the strip is cut along the dotted lines opposite... |
 |
| ... and the pieces 1 and 2 are moved like opposite... | 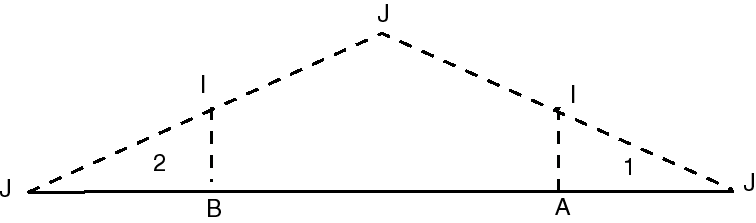 |
| ...the we get a less classic triangular representation
of the Möbius strip.
Here, the oriented segment line [J1 J2] is identified to [J3 J1], so that the 3 points J1, J2, J3 are identified. Here, it is easier to see the unique boundary. |
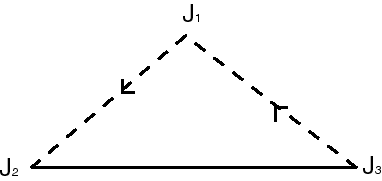 |
| Another way of obtaining the Möbius strip: take a circular ring and identify the points that are symmetric about the center (a half-ring is then equivalent to a rectangle where two widths are identified, in opposite directions, which indeed gives a Möbius strip) |
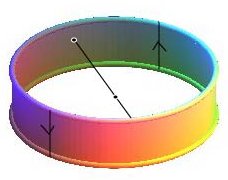 |
| Consider the sphere where the antipodal points are identified,
i.e. a real projective plane.
Then, a strip located between to tropics is a Möbius strip. The complement
is an open disk.
The Möbius strip can therefore be obtained by puncturing
an open hole into a projective plane.
|
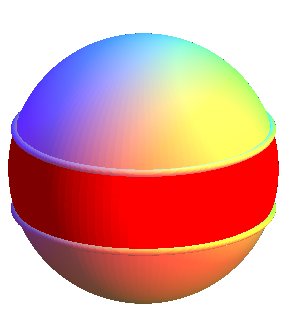 |
| This is why the punctured cross-cap
is a Möbius strip (or rather, an immersion of a Möbius strip,
because of the self-intersection), see opposite:
Inversely, when a Möbius strip and a disk are sewed
together by their boundary, we get a real
projective plane that can be immerged in |
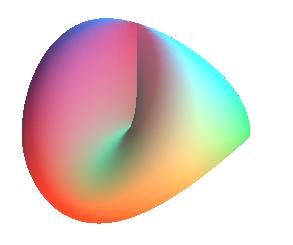 or or |
The chromatic number of the Möbius strip is therefore equal to that of the projective plane, i.e. 6.
When two Möbius strips are sewed together by their
boundaries, we get the connected sum of two real projective planes, i.e.
a Klein bottle.
 +
+ |
 =
= |
 |
The Möbius strip without its boundary is called the
open Möbius strip; it is homeomorphic to the projective plane minus
one point.
| The Möbius strip can be represented by a union of three non coplanar polygons, necessarily non convex, as opposite (see Brehm's polyhedron): |
 |
See also the boundary of the Möbius strip with 3 half-twists, which is a trefoil knot and the fake Möbius strip on the torus.
The engraver M.C.
Escher worked a lot on the Möbius strip:

Escher's famous Möbius strip. |
 this way he gets only one strip, knotted like a trefoil knot, with 6 half-twists. |
 |
 |
| Escher's famous horsemen are represented on a strip with two half-twists, hence with two faces (colored in grey and beige) and two boundaries, but the central fusion that simulates the identification between two segment lines of each boundary (indicated in green) makes it a topological Möbius strip with only one face, and only one boundary, indicated in red (cf. Möbius shorts) | Same principle for these swans with black-and-white faces. |
| Möbius strip braided with only one braid by Juan Pablo Baudry | Möbius strip with 3 half-twists knotted as a trefoil
knot.
University of Flensburg. |
|
Jos Leys created an animation based on Bach's canon of musical offerings, which can be read in both directions. Watch the video. |
|
|
 |
 |
 |
Like the Borromean rings, the Möbius strip is a strong symbol, hence the many logos:

Logo of recycled products: 1 half-twist, cf. the strip with 3 cylinders above |
Logo of the Léman Express, RER in Geneva left-handed with one half-twist |

Logo of Commerzbank left-handed strip with 3 half-twists |

Logo of the Swiss institute of intellectual property, the title of which is written in the four national languages. |

Logo of a German university left-handed strip with 3 half-twists |
|
Canadian Mathematical Society |
|

 |
 |

The logo of Renault is a strip with two half-twists, and therefore is not a Möbius strip |
 |

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Samuel BOUREAU, Alain ESCULIER, Christoph SOLAND 2017