NŒUD DE TRÈFLE
Trefoil
knot, Kleeblattschlinge
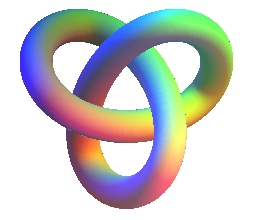
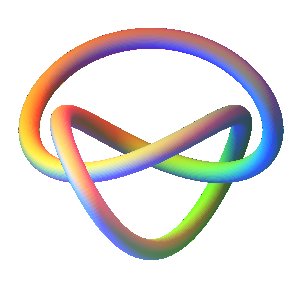
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
NŒUD DE TRÈFLE
Trefoil
knot, Kleeblattschlinge
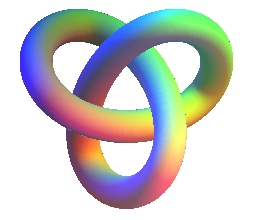
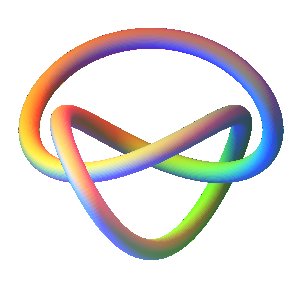
| Sites :
Knot atlas etacar.put.poznan.pl/piotr.pieranski/IdealKnots.html |
 |
Représentation cartésienne dont la projection
sur xOy est une hypotrochoïde
: |
 |
Représentation par solénoïde
torique de coefficient n = 3/2 : |
 |
Autre représentation : 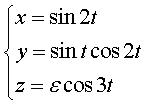 . .
Voir aussi ici un noeud de trèfle ouvert. |
Le noeud de trèfle est l'unique noeud dont le nombre minimal de croisements est minimal, à savoir 3 ; il en existe en fait deux, énantiomorphes (images l'un de l'autre par réflexion).
C'est un demi-noeud
de cordage :  dont on a relié les extrémités.
dont on a relié les extrémités.
Le noeud de trèfle est aussi le noeud torique de type (3,2) (3 enroulements autour du tore, sur deux tours), ainsi que celui de type (2,3) :

noeud torique à 3 enroulements sur 2 tours |
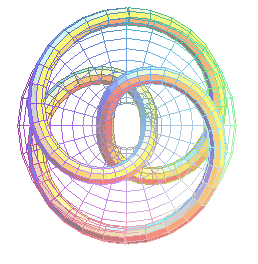
noeud torique à 2 enroulements sur 3 tours ; contrairement aux apparences, on obtient le noeud de trèfle et non le noeud en huit. |
| Le noeud de trèfle est le bord d'un ruban de Möbius à 3 demi-torsions. |
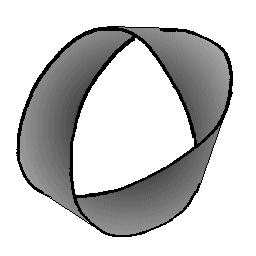 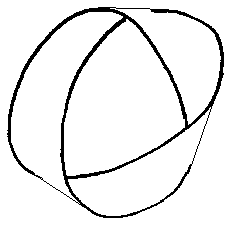 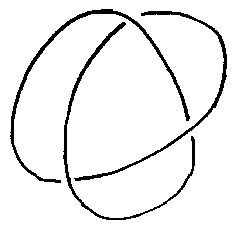 |
| Inversement, une bande nouée en noeud de trèfle peut donner un ruban de Möbius (noter ici les 3 demi-torsions) ; il s'agit de 3 bandes accolées découpées dans des cônes non circulaires, de directrice une courbe de Viviani et dont les sommets sont ceux du triangle rouge indiqué. L'ensemble est donc développable, mais le développement n'est pas rectiligne. |
 |
| Tracé de la bande
développable centrée sur la courbe [cos(u)+2*cos(2*u),sin(u)-2*sin(2*u),2*sin(3*u)],
qui se développe donc en un rectangle, et qui donne pile un ruban
de Möbius.
Sauf que nous avons légèrement triché pour le raccordement qui ne se fait pas bord à bord mathématiquement, comme on voit ici... |
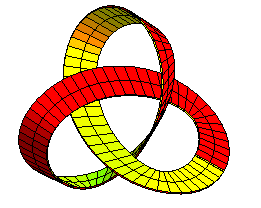 |
| Noeud de trèfle obtenu par pliement d'une bande
rectiligne.
Le ruban présente 6 demi-tours, donc n'est pas un ruban de Möbius (il a deux faces, et deux bords). (Logo du point gamma, soirée étudiante de Polytechnique). |
 |
| Ci-contre, un noeud de trèfle obtenu par une ligne polygonale gauche fermée à 6 segments ; contrairement aux apparences, les 6 barres ne sont pas de la même longueur (les 3 barres extérieures sont plus courtes). |
 |
Ci-contre, un noeud de trèfle obtenu par 6 segments
de même longueur ;
les coordonnées des 6 points a,b,c,d,e,f sont : [[-1, 0, 0], [1, 0, 0], [(13-4*22^(1/2))/25, 6/5, -(4/25)*(-1+22^(1/2))*3^(1/2)], [-1/2, 3/5, (1/2)*3^(1/2)], [1/2, 3/5, -(1/2)*3^(1/2)], [(-13+4*22^(1/2))/25, 6/5, (4/25)*(-1+22^(1/2))*3^(1/2)], [-1, 0, 0]]: |
|
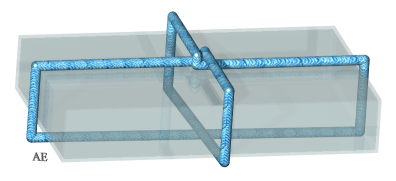
| Il est démontré qu'il est impossible d'obtenir un noeud de trèfle à 5 barres, excepté dans la figure impossible ci-contre (idée d'Alain Esculier, à la manière d'Oscar Reutersvärd.). |  |
Pour 6 barres, impossible également que les segments soient deux à deux parallèles, sauf de nouveau pour cette figure impossible | 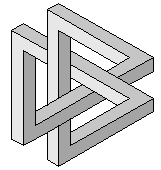 |
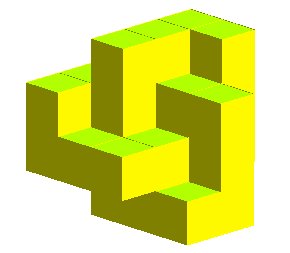
| Ci-contre, plusieurs vues d'un noeud de trèfle
formé de lignes polygonales à angles droits.
On démontre que cette figure représente le plus petit noeud de trèfle passant par les sommets d'un réseau cubique. |
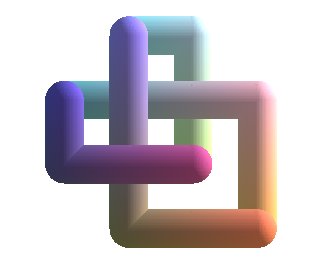 |
 |
 |
| Deux autres versions polygonales à 9 et 12 segments. |  |
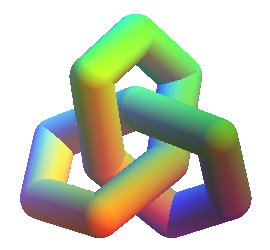 |
| L'appellation "noeud de trèfle" est probablement due à la ressemblance des représentations ci-contre avec une feuille de trèfle : |
 |
 |
| Ce noeud à 4 croisements apparents est un noeud
de trèfle (tournez la boucle du haut pour faire disparaître
le croisement central).
Inversez les deux croisements du haut (ou du bas) et vous obtenez un noeud de huit. |
 |
| La ficelle de ce paquet forme un noeud de trèfle (mais si l'on inverse un croisement, le noeud devient trivial). |
 |
| Ce motif de type ornement mongol, forme un noeud de trèfle (un croisement est supprimable). |
 |
| On pourrait désigner par "noeud de trèfle
à 4 feuilles" la courbe dont la projection sur xOy est une
hypotrochoïde
à 4 feuilles, de paramétrisation : |
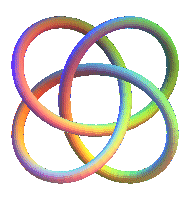 |
| Ceci peut se généraliser au "noeud de trèfle
à n feuilles" : |
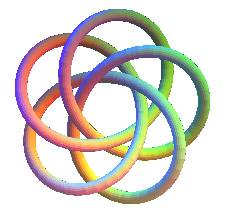 |
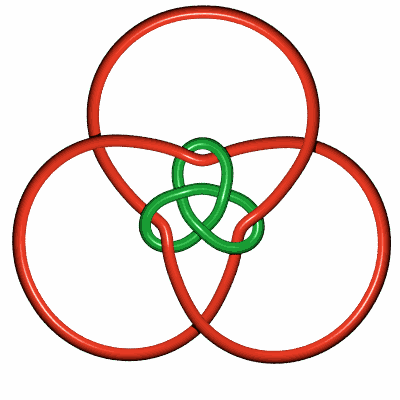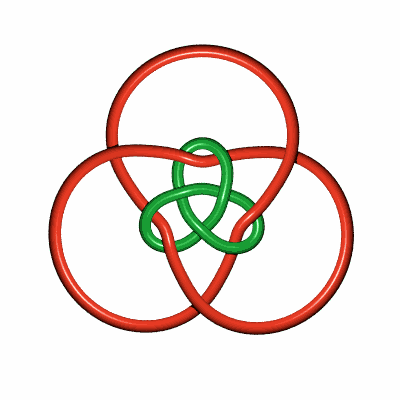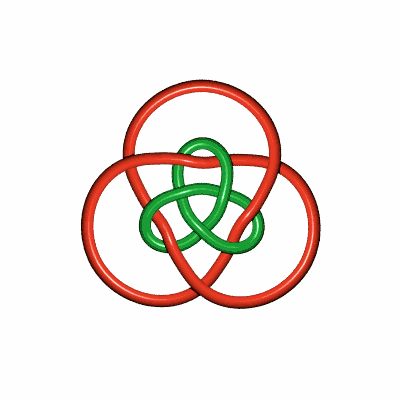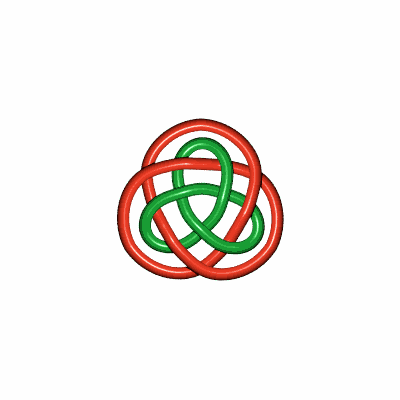
| Si on double le brin constituant le noeud de trèfle,
on obtient ce bel entrelacs à
12 croisements.
(idée d'Alain esculier) |
 |
| Cette somme de deux noeuds de trèfle, donc un
noeud
plat, a été obtenue à partir de la courbe de paramérisation
: |
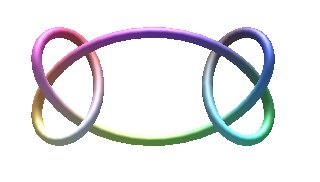 |
Voir aussi les deux graphes associés au noeud de trèfle, la surface de Seifert associée, les noeud plats, et "de vache", sommes de deux noeuds de trèfle.
Le noeud de trèfle dans l'art :
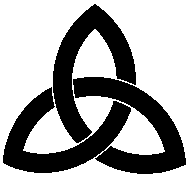 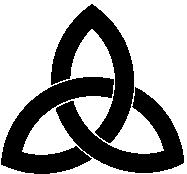
Le noeud celtique simple est un noeud de trèfle. |
  |

Le noeud de trèfle vu par Escher. |

Sculpture en noeud de trèfle, université de Flensburg.
|
Le noeud de trèfle est souvent utilisé comme
logo :
 |
 |
|
 |
||
|

Logo du Cimat, centre de recherche mathématique à Guanajuato, Mexique. |

Derrière le logo Woolmark, on peut imaginer un noeud de trèfle... |
 |
||
|
Logo de la région Haut-de-france |

 |
||||
|
Noeud de trèfle celtique entrelacé
avec un noeud trivial.
|
 |

Noeud de trèfle extra-terrestre ! |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2015