Et inversement tout graphe planaire 4-régulier
est la projection d'un entrelacs.

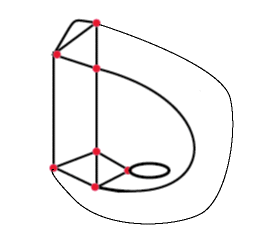
...vue comme un graphe 4-régulier.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
GRAPHE ASSOCIÉ À UN ENTRELAC
link
graph, Verschlingungsgraph
| Liens :
Wikipedia Article de Christian Mercat |
| La projection sur un plan d'un entrelac
est dite générique si les points de croisements sont
tous doubles à tangentes distinctes. On peut alors la considérer
comme un graphe
planaire dont tous les sommets sont de degré 4.
Et inversement tout graphe planaire 4-régulier
est la projection d'un entrelacs.
|
 |

...vue comme un graphe 4-régulier. |
| Pour pouvoir reconstituer l'entrelac, il faut indiquer
quel brin passe dessus et lequel passe dessous, en arrêtant le tracé
du brin inférieur. Une telle figure est appelée diagramme
de
l'entrelacs.
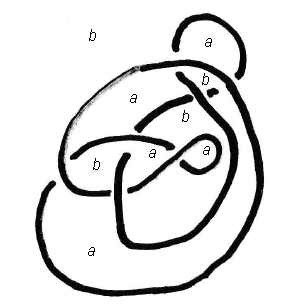
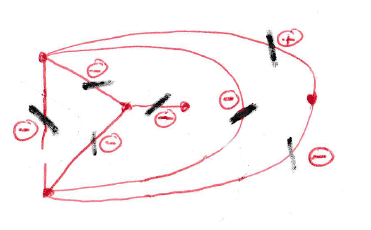
On peut aussi "étiqueter" les sommets de sorte à retrouver le type du passage, de la façon suivante : le graphe, ayant tous ses sommets de degré pair, a ses faces coloriables en deux couleurs, ici a et b. Les sommets sont alors décrétés positifs ou négatifs par les conventions ci-contre (évidemment, l'échange des deux couleurs échange les + et les –). A tout graphe planaire 4-régulier à sommets étiquetés + ou – correspond donc un unique entrelac. Remarquons que l'entrelac est alterné (passages dessus-dessous successifs) ssi les sommets du graphe sont tous du même signe.
|
 |
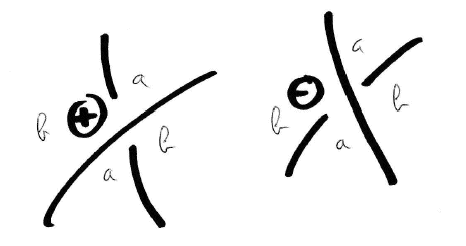 |
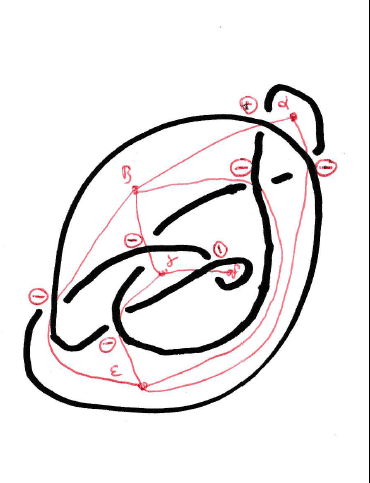
| Le graphe associé au diagramme d'entrelac
(Peter Tait,1880) a pour sommets les faces d'une couleur donnée
(par exemple
a), deux faces étant reliées par une
arête si elles ont un point de croisement du digramme en commun.
C'est un graphe planaire (pouvant avoir des arêtes multiples) que l'on obtient concrètement en plaçant un point au "centre" de chaque face et en reliant ces points par des chemins passant par les croisements. Chaque arête de ce graphe est décrétée du signe du sommet traversé. On peut inversement récupérer l'entrelacs à partir du graphe à arêtes "signées", comme indiqué dans la figure de droite. Si l'on choisit les faces de l'autre couleur, le graphe obtenu n'est autre que le dual du graphe précédent. |
 |
 |
Voici des exemples classés par nombre d'arêtes,
donc par nombre de croisements de l'entrelac, lui-même choisi alterné.
Dans le codage a.b.c , a est le nombre
de croisements, b le nombre de brins, c le numéro
d'ordre donné par Rolfsen.
DEUX ARÊTES ou CROISEMENTS
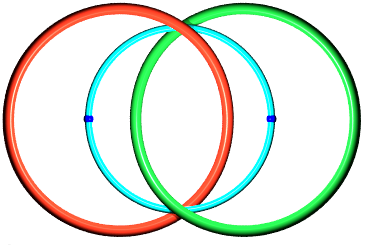
| L'entrelac de Hopf 2.2.1 est associé au graphe à deux sommets reliés par une arête double. Ce graphe est autodual. |
 |
TROIS ARÊTES ou CROISEMENTS
| Nom du noeud ou de l'entrelac | Graphe en bleu, entrelac associé en rouge | Figure avec le graphe dual du précédent |
| Noeud de trèfle 3.1.1 |
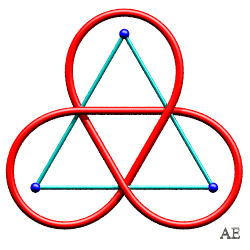 |
 |
QUATRE ARÊTES ou CROISEMENTS
| Nom du noeud ou de l'entrelac | Graphe en bleu, entrelac associé en rouge et vert | Figure avec le graphe dual du précédent |
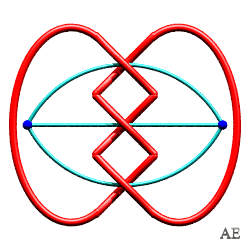
| Noeud de Salomon 4.2.1 |
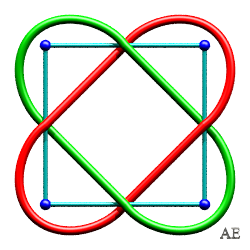 |
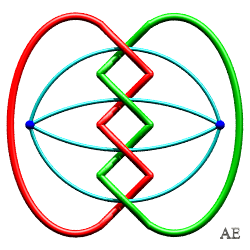 |
| Noeud de huit 4.1.1 |
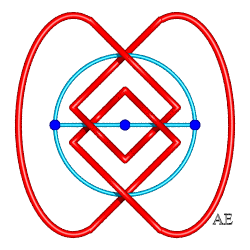 |
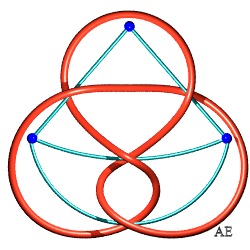 |
CINQ ARÊTES ou CROISEMENTS
| Nom du noeud ou de l'entrelac | Graphe en bleu, entrelac associé en rouge et vert | Figure avec le graphe dual du précédent |
| Noeud 5.1.1 |
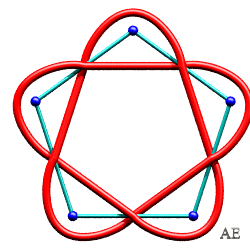 |
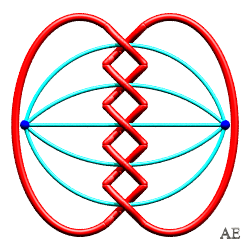 |
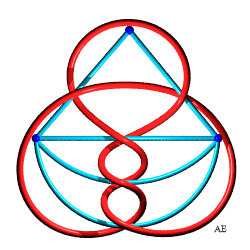
| Noeud 5.1.2 |
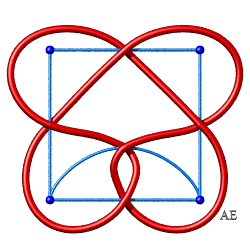 |
 |
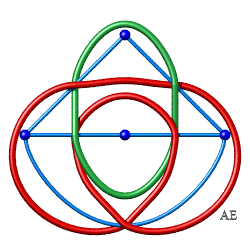
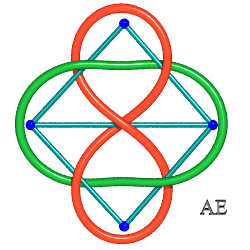
| Entrelacs de Whitehead 5.2.1 |
 |
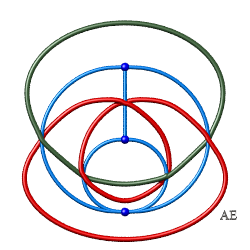
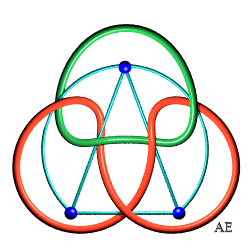 |
Autres exemples :
| L'entrelac torique T(n,2) a pour graphe le graphe circulaire à n arêtes simples positives : |
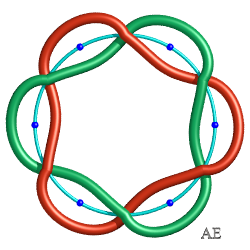 |
| Si les arêtes sont multiples, on obtient un entrelac de bretzel : |
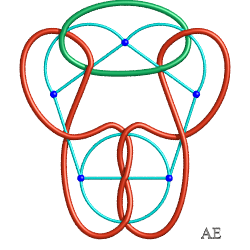 |
| L'entrelac de billard rectangulaire de type (p,q) a pour graphe une grille rectangulaire de p – 1 cases sur q – 1 cases ; ci-contre le cas (5,3). |
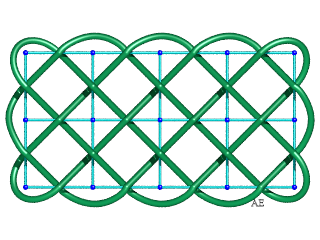 |
| L'entrelac
de billard cylindrique ou bonnet turc de type (p,q) a pour graphe
une grille circulaire formée de Ci-contre par exemple, les cas (5,3) et (5,4). |
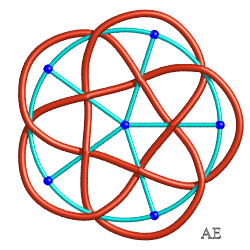 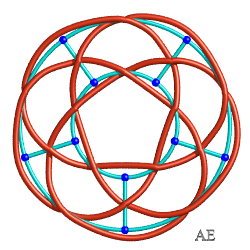 |
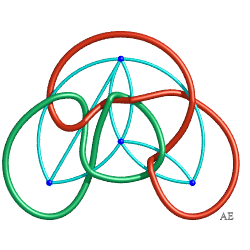
| Tout plongement dans le plan d'un (multi)graphe planaire
donne donc naissance à un unique entrelac. On peut se demander :
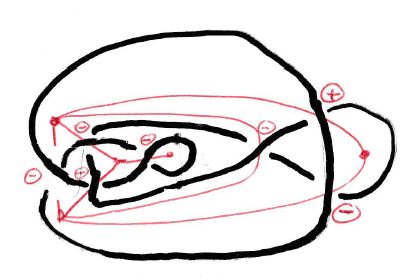
1) Si deux plongements du même graphe abstrait donnent forcément naissance à deux entrelacs équivalents. 2) Si deux graphes non isomorphes donnent naissance à deux entrelacs non équivalents. La réponse à ces questions est malheureusement "non" : - les deux noeuds K11a57 et K11a231 bleus ci-contre ont le même graphe associé, mais ne sont pas équivalents (ce sont des "noeuds mutants"). - les deux graphes bleus pastel indiqués ci-contre ne sont pas isomorphes (l'un a un sommet de degré 6 et l'autre non) mais les deux entrelacs associés sont équivalents : entrelacs 8.2.7. |
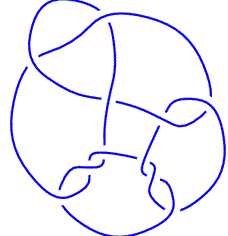 
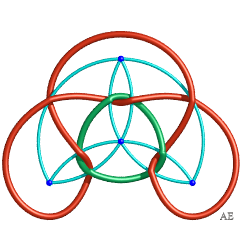  |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Alain ESCULIER 2022