HÉLICE ou COURBE DE PENTE CONSTANTE
Helix
or curve of constant slope, Böschungslinie oder Kurve von konstanter
Steilheit
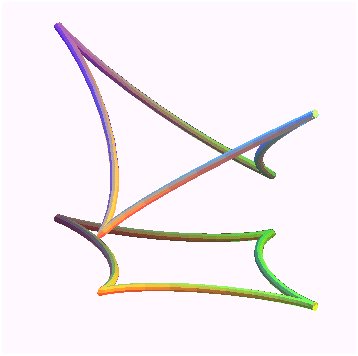
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
HÉLICE ou COURBE DE PENTE CONSTANTE
Helix
or curve of constant slope, Böschungslinie oder Kurve von konstanter
Steilheit
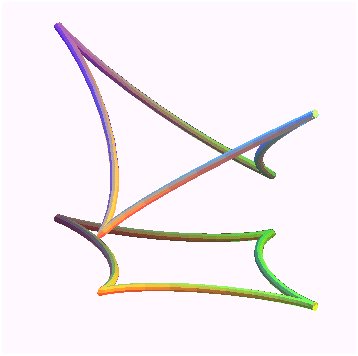
| Du latin "helix", issu lui même du grec "eliks"
: spirale.
Autres noms : courbe d'égale pente, courbe isocline. |
| Le plan fixe étant xOy , condition différentielle : | |
| soit en coordonnées cartésiennes : | |
|
Paramétrisation cartésienne connaissant la base de l'hélice, de paramétrisation |
|
| Rayons de courbure et de torsion, |
|
| Equation différentielle des hélices tracées
sur la surface |
|
|
Équation cylindrique des hélices tracées sur la surface de révolution |
Les hélices sont les courbes dont les tangentes
font un angle constant a avec un plan fixe (P0),
ou avec une direction fixe d (orthogonale à
(P0)).
La notion d'hélice en mathématiques a donc
plus de rapport avec une route de montagne de pente constante qu'avec une
hélice de bateau !
Concrètement, on obtient une hélice mathématique
en découpant dans du carton un triangle rectangle
que l'on fait tenir verticalement sur un plan puis que l'on déforme
: l'hypothénuse prend une forme d'hélice.
Conditions nécessaires pour qu'une courbe soit
une hélice :
- courbe dont l'indicatrice
sphérique de courbure est plane (donc incluse dans un cercle).
- courbe dont les normales principales restent
parallèles à un plan fixe (égal à (P0)).
- courbe dont les binormales font un angle constant
avec une direction fixe (la même que les tangentes).
- courbe dont l'indicatrice
sphérique de torsion est plane (donc incluse dans un cercle).
- courbe dont la torsion est proportionnelle à
la courbure (théorème
de Lancret).
- trajectoire d'un mouvement dont les vecteurs
dérivés second, troisième et quatrième sont
coplanaires.
- géodésique
d'un cylindre (le cylindre engendré par les parallèles à
d)
- autrement dit, si l'on développe le cylindre sur lequel l’hélice
est tracée, l'hélice devient une droite.
Une hélice est entièrement définie par la donnée de sa projection dans (P0) (sa base) et l'angle a.
Exemples (on notera que les hélices sont désignées
soit par rapport à leur base, soit par rapport à la surface
sur laquelle elles sont tracées) :
- la droite (les droites d'une surface
sont donc des hélices de cette surface)
- l'hélice
circulaire (base = cercle)
- l'hélice
conique (tracée sur un cône de révolution vertical,
base = spirale logarithmique)
- l'hélice
elliptique (base = ellipse)
- l'hélice
sphérique (tracée sur la sphère, base = épicycloïde)
- l'hélice
du paraboloïde (tracée sur le paraboloïde, base =
développante de cercle)
- l'hélice
du H1
(tracée sur l'hyperboloïde à une nappe)
- La ligne
de striction du berlingot
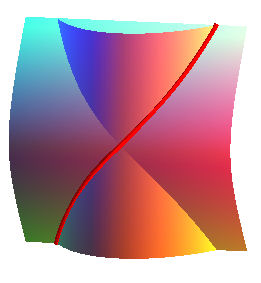
| - l'hélice caténoïdique
(base = chaînette ) : elle est tracée sur le cylindre hyperbolique Courbe étudié par Catalan en 1878. L'hélice caténoïdique est la génératrice de l'hélicoïde minimal. |
 |
| - l'hélice torique (tracée
sur le tore, le plan de référence
étant orthogonal à l'axe du tore) :
|
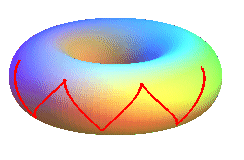
Hélice de pente 1 du tore |
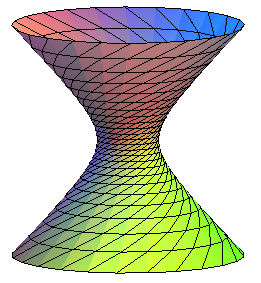
| Exemple de détermination des hélices d'une
surface : celles de l'hyperboloïde
de révolution : x² + y² = z² +1, paramétré
par
x = ch u cos v, y = ch u sin v, z = sh u. On écrit que dz/ds = tan a, soit dx²
+dy² = dz² cot² a, soit ici :
soit racine(cot²a - th² u)
du = dv, d'où l'on tire v en fonction de u : Pour a = pi/4 on retrouve les droites incluses. Ci-contre ont été tracées les hélices
pour cot a = 2, voir la page correspondante.
|
 |
Voir aussi les surfaces d'égale pente.
Ont été définies d'autres type d'hélices,
comme par exemple les "slant helices" qui sont les courbes dont la normale
principale (et non la tangente) fait un angle constant avec un plan (ou
une direction) fixe, voir cet
article, et celui-ci.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2024