next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

HELIX or CURVE OF CONSTANT SLOPE

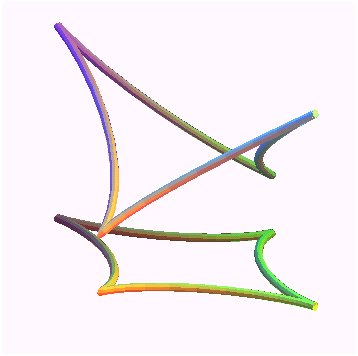
Une hélice de base astroïdale

From the Latin "helix", derived itself from the Greek "eliks": spiral.
Other names: curve of equal slope, slope line, isocline curve.

 
The fixed plane being xOy, differential condition: 
i.e. in Cartesian coordinates: 

Cartesian parametrization knowing the base of the helix, parametrized by : 
Radii of curvature and torsion,  being the radius of curvature of the base: et 
Differential equation of the helices traced on the surface , using the Monge notations:  coming

Cylindrical equation of the helices traced on the surface of revolution : 

The helices are the curves the tangents of which form a constant angle a with respect to a fixed plane (P0), or a fixed direction d (orthogonal to (P0)).
Therefore, the notion of helix in mathematics is more connected to a mountain road with constant slope than to the helix of a boat!
Concretely, we get a mathematical helix by cutting a right triangle  out of a cardboard, placing it vertically on a plane and deforming it: the hypothenuse takes the shape of a helix.

Necessary conditions for a curve to be a helix:
 - curve for which the spherical indicatrix of curvature is planar (therefore included in a circle).
 - curve the principal normals of which remain parallel to a fixed plane (equal to (P0)).
 - curve the binormals of which form a constant angle with respect to a fixed direction (the same as the tangents).
 - curve for which the spherical indicatrix of torsion is planar (therefore included in a circle).
 - curve the torsion of which is proportional to the curvature (Lancret theorem).
 - trajectory of a movement for which the second, third and fourth derivative vectors are coplanar.
 - geodesic of a cylinder (the cylinder generated by the lines parallel to d) - in other words, if we develop the cylinder on which the helix is traced, the helix becomes a straight line.

A helix is entirely defined by its projection on (P0) (its base) and the angle a.

Examples (note that the helices are described by their base or the surface on which they are traced):
    - the straight line (lines on a surface are therefore helices of this surface)
    - the cylindrical helix (base = circle)
    - the conical helix (traced on a vertical cone of revolution, base = logarithmic spiral)
    - the elliptic helix (base = ellipse)
    - the spherical helix (traced on a sphere, base = epicycloid)
    - the helix of the paraboloid (base = involute of a circle).
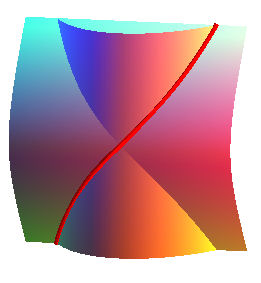
    - the helix of the one-sheeted hyperboloid (traced on the one-sheeted hyperboloid)
    - the striction line of the milk carton
 
   - the catenary helix (base = catenary): ();
it is traced on the hyperbolic cylinder , as well as the surface , which is a surface of revolution when a = b.
Curve studied by Catalan in 1878.
The catenary helix is the generatrix of the minimal helicoid.

 
     - the torus helix (traced on the torus, the reference plane being orthogonal to the axis of the torus):

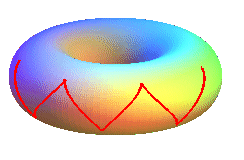
Torus helix with slope 1

 
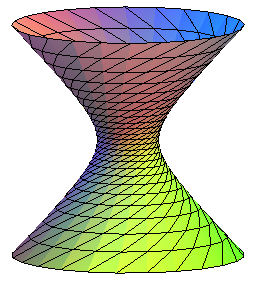
Example of determination of the helices on a surface: those of the hyperboloid of revolution: x² + y² = z² +1, parametrized by

x = cosh u cos v, y = cosh u sin v, z = sinh u.

Write dz/ds = tan a, i.e. dx² +dy² = dz² cot² a, hence, here:
 sinh² u du² +cosh²u dv² = cosh² u cot² a du²

i.e.    sqrt(cot²a - tanh² u) du = dv, from which we get v as a function of u.

For a = pi/4 we get the included lines.

The helices with cot a = 2 were traced opposite.
 

See also the surfaces of equal slope.

Other types of helices have been defined, such as "slant helices" which are curves whose main normal (and not the tangent) makes a constant angle with a fixed plane (or direction), see this article, and this one.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2024