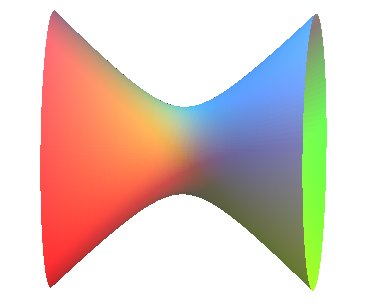
ONE-SHEETED HYPERBOLOID H1
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ONE-SHEETED HYPERBOLOID H1

| Surface studied by Christopher Wren in 1669. |
(see [Struik, p 195] ) Gaussian curvature: Directrix cone, which also is the asymptote cone: Volume for 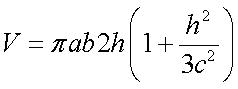 . .
Case of the rectangular hyperboloid (a = b) Cylindrical equation: First fundamental quadratic form: |
The one-sheeted hyperboloid can be defined as:
1) a ruled quadric
with a center of symmetry.
2) the union of the lines meeting three lines 2
by 2 non-coplanar and non-parallel to a fixed plane (when they are, we
get the hyperbolic
paraboloid)
3) the union of the lines (MN), when the
points M and N move at constant speed on two parallel circles.
Here, the hyperboloid is the union of the lines
and
and is also the union of the lines
and
.
The sections of the hyperboloid by vertical planes tangent
to the inside ellipse are the pairs of secant lines from the two families
of included lines.
| Parametrization of the hyperboloid generated by the lines
joining a circle of radius a to a circle of radius b distant
by h from the first and turned at an angle Volume of the trunc of the corresponding hyperboloid: |
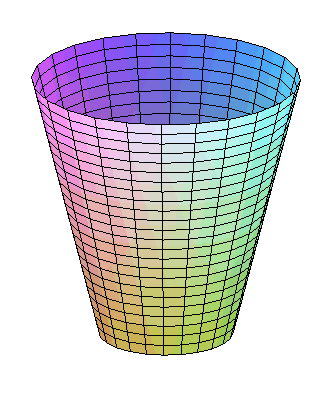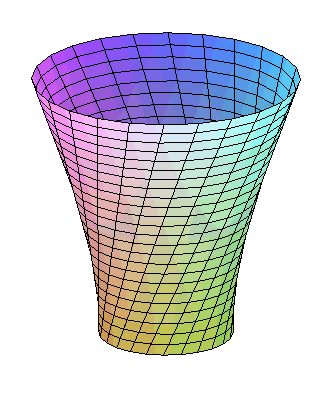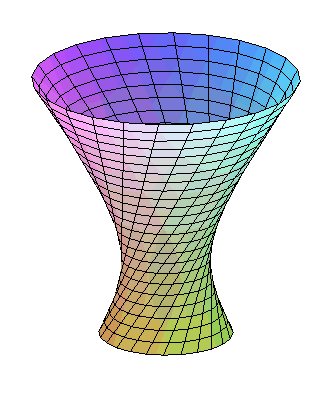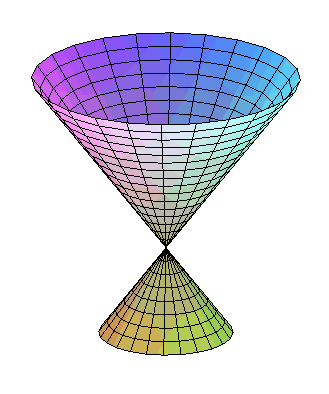 |
The one-sheeted hyperboloid of revolution can be
defined as the surface of revolution generated by a line non-coplanar with
the axis of revolution, or as the surface of revolution generated by the
rotation of a hyperbola
around its non-transverse axis.
 |
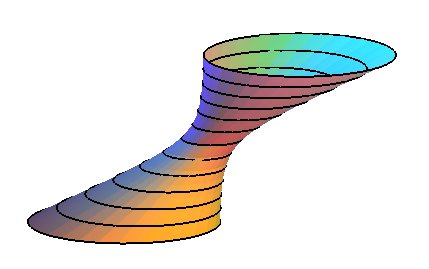
View of the curvature
lines of the one-sheeted hyperboloid; they are circles and hyperbolas
only in the case of the hyperboloid of revolution.
Otherwise, they are biquadratics. |
 |
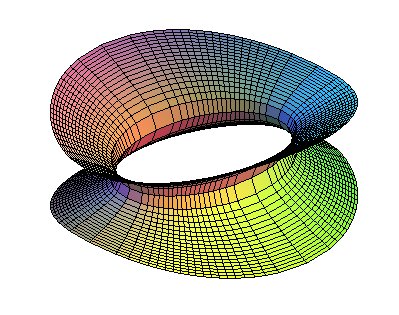
View of one of the two families of circles included in any H1, even if it is not of revolution. |
See here helices of the hyperboloid, as well as the curves of constant precession, traced on a hyperboloid.
Because of its property of being the union of lines, the
one-sheeted hyperboloid, like the hyperbolic
paraboloid is often used in architecture.

Cooling towers of nuclear power plants. |
Water tower in La Roche de Glun in Drome |

|
 |
|
 |
See more beautiful pictures on the mathourist's
page.
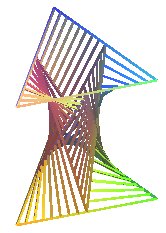    
Structure designed from 2 regular polygons with n sides and 2n generatrices of a hyperboloid of revolution (joining 2 middles of sides of these polygons). The 3n resulting skew diamonds are filled by generatrices of hyperbolic paraboloids. (production: Alain Esculier) |
 |
 |
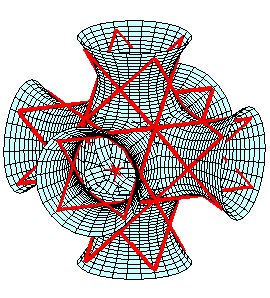 |
| When two "solid spaces" have uniform rotation motions
with non-secant axes, the two loci of the instant axes of rotation of their
relative motion in each of the spaces (or "axoids") are two hyperboloids
of revolution that roll without slipping on one another (spatial notion
equivalent to that of mating
gear profile in the plane).
This beautiful kinematics theorem is at the origin of the "hyperboloidal gears" an example of which is reproduced opposite: See this book, page 144. |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL2017