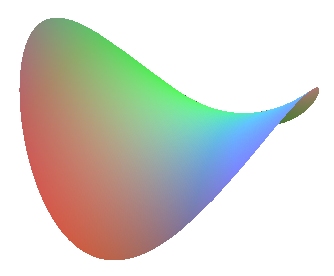
HYPERBOLIC PARABOLOID
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
HYPERBOLIC PARABOLOID
Informal names: HP bowl, or horse saddle  ,
or Pringles:  . |
Cartesian equation:  .
Doubly ruled quadric. Cartesian parametrization:
Striction
lines: the 2 parabolas sections by the planes |
| The paraboloid is said to be rectangular if a
= b (the generatrices of each family are then perpendicular two
by two).
Cartesian equation in the rectangular case: 
(frame turned by 
around Oz,  ).
Cylindrical equation:  .
Cartesian parametrizations:
 .
Surface element:  .
Second fundamental quadratic form:  .
Gaussian curvature:  ;
all the points are hyperbolic.
Mean curvature:  . |
The hyperbolic paraboloid can be defined as the
ruled
surface generated by the straight lines
- meeting two lines that are non coplanar
and remaining parallel to a fixed plane (secant to these two lines) called
directrix plane of the paraboloid
- meeting three lines that are two
by two non coplanar, but parallel to a given plane (when it is not the
case, we get the one-sheeted
hyperboloid).
| A hyperbolic paraboloid can also be defined as the union
of the lines joining two points moving at constant speed on two non coplanar
lines.
The 4 sides of any skew quadrilateral are therefore included in a unique HP (see this link for details); unfortunately, this HP is not the surface with minimal area supported on this contour (see a special case at Schwarz surface). See also milk carton. |
  |
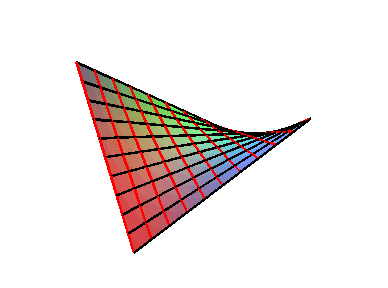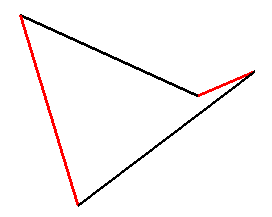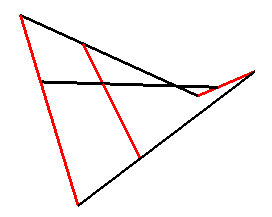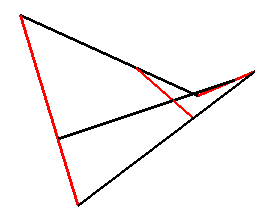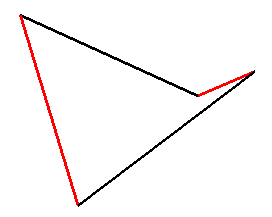| A portion of paraboloid can therefore be produced by tightening elastic bands between two linear rods (with a smooth connection between the elastic bands and the rods). |
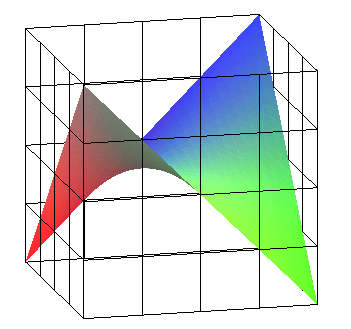
In the equations above, the paraboloid is the union of
the lines 
parallel to the directrix plane (which is also an asymptote) (P): 
and also the union of the lines 
parallel to the directrix plane (P'): 
.
The hyperbolic paraboloid is doubly a conoid;
more precisely, it is a conoid with axis one of the lines 
,
directrix plane (P') and directrix another line ,
and a conoid with axis one of the lines 
,
directrix plane (P) and directrix another line .
The rectangular case (a = b) corresponds
to the case of the right conoid, and it is a special case of generalized
Zindler conoid.
It is also a translation surface (translation of a parabola along another one, oriented in opposite directions).
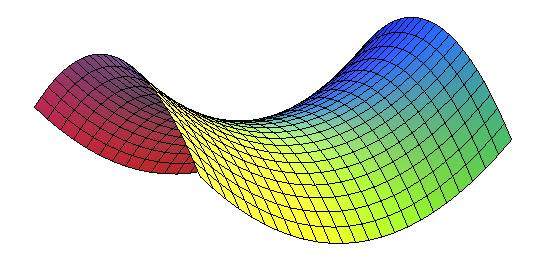
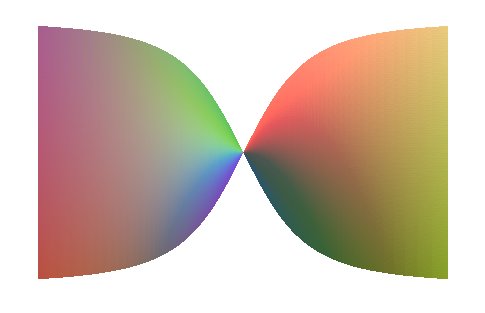
The sections by planes parallel to Oz are parabolas, and the other planar sections are hyperbolas or lines.
In the rectangular case, the sections by cylinders with
axis Oz are pancake
curves.
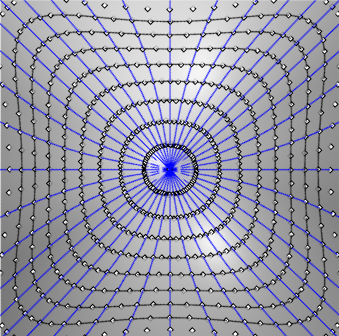
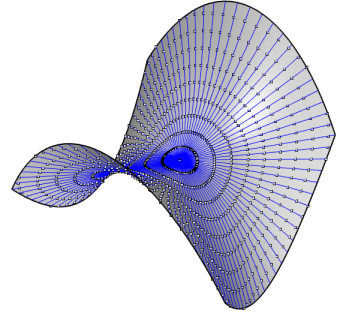
The projections on xOy of the geodesic
lines of the equilateral HP z = xy are the curves solutions
of the differential equation :  .
You can see on this picture the geodesic lines coming from O and the corresponding "geodesic circles". |
 |
 |
| Confocal paraboloids and triple orthogonal family of
paraboloids.
If a > b, then the paraboloids with equation |
 |
See also the flippable
surfaces, the Bezier surfaces
and the monkey saddle.
Playground for children, boulevard Richard Lenoir, Paris. The ropes follow (more or less) the Cartesian parametrization by the straight lines... |
Here, Place Bellecour, Lyon. The ropes follow the polar parametrization, by parabolas and pancake curves. |
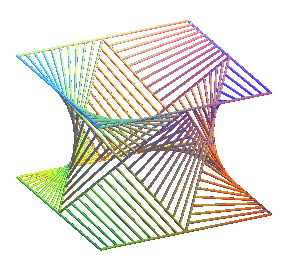 Structure composed of 12 portions of hyperbolic paraboloids; the 8 oblique
generatrices (joining 2 middles of a side of a square) are generatrices
of a hyperboloid of revolution.
|
Sculpture by Angel DUARTE made of pieces of hyperbolic paraboloids (Lausanne, Switzerland) using this structure. It has 36 portions of hyperbolic paraboloids. |
Explanation of this structure. Compare to the Schwarz P minimal surface. |
Restaurant Los Manantiales, Mexico Architect: F. Candela 1958  |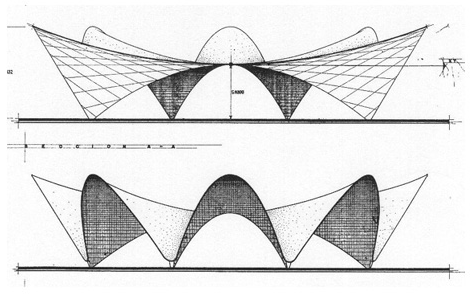
Vaults inside the Sagrada Familia, Barcelona.
|
Church of Becerril de la Sierra, Spain Architect: Friar Francisco Coello de Portugal |
Palais du Cnit, Paris, the shape of which reminds the hyperbolic paraboloid, is in fact, as a first approximation, the union of three parabolic cylinders. |
See more beautiful pictures on the mathourist's
page.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
or
.
where 
(linear and located in the plane z = 0 in the rectangular case).
or 
are such that the sections by the plane xOz are confocal parabolas
(i.e. with the same focus 
).
we get a first family, composed of elliptic paraboloids, for 
we get a second family, composed of hyperbolic paraboloids, for 
,
we get a third family, composed again of elliptic paraboloids.