Monkey saddle

MONKEY SADDLE

Cylindrical equation:

.
Cartesian parametrization:

.
Cartesian equation:

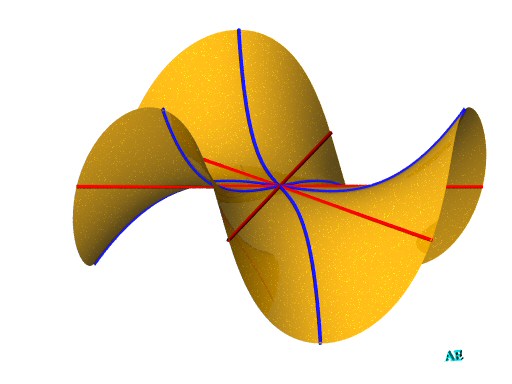
Surface shaped like a saddle that allows to place a monkey's legs but also its tail (the monkey is not the mount, but the rider!).

By the point O (which is a planar point of the surface) there pass 3 real lines of the surface, forming between one another angles of 120° (in red above): the point O is an Eckardt point of the surface; by the point at infinity of Oz, which is a singular point of the surface, there pass the 3 other lines of the surface, that are also real, but at infinity.
O is also an umbilic.

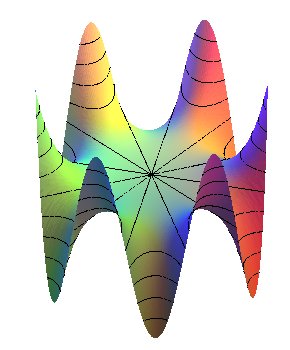
Generalization: surface with a saddle where end n valleys and n mountains: (hence a surface with rotational symmetry).
The case n = 2 gives the horse saddle or hyperbolic paraboloid and the case n = 3 the monkey saddle.
Proposition of name by Paul Micaelli: octopus saddle...

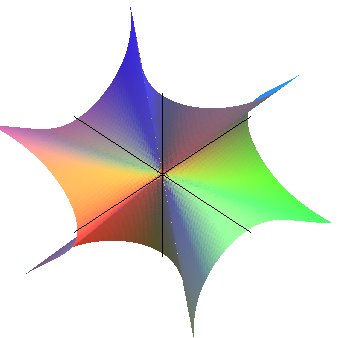
Other surface with 3 valleys, 3 mountains: ; but the saddle is not comfortable, there is no tangent plane at O (it is a cone, cf. Cartan's umbrella).

Surface with 4 mountains, 4 valleys, flat this time : ; named "crossed trough".

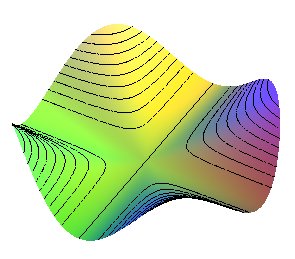Compare to the Enneper surface.

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra

Generalization: surface with a saddle where end n valleys and n mountains: (hence a surface with rotational symmetry). The case n = 2 gives the horse saddle or hyperbolic paraboloid and the case n = 3 the monkey saddle. Proposition of name by Paul Micaelli: octopus saddle...
Other surface with 3 valleys, 3 mountains: ; but the saddle is not comfortable, there is no tangent plane at O (it is a cone, cf. Cartan's umbrella).
Surface with 4 mountains, 4 valleys, flat this time : ; named "crossed trough".