CLEBSCH (DIAGONAL CUBIC) SURFACE
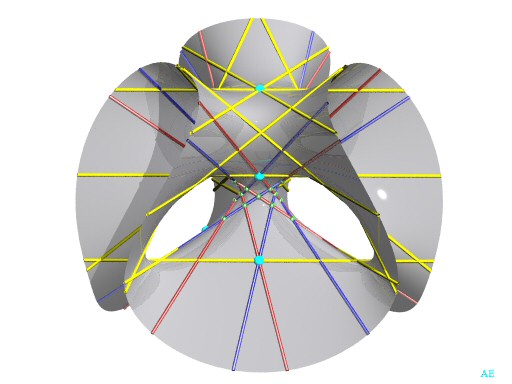
In yellow the 15 diagonals with the Eckardt points, in red and blue
the principal double six.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CLEBSCH (DIAGONAL CUBIC) SURFACE

In yellow the 15 diagonals with the Eckardt points, in red and blue
the principal double six.
| Surface studied by Clebsch in 1871.
Alfred Clebsch (1833-1872): German mathematician. |
| Pentahedral equation in Smooth cubic surface with hyperbolic points. |
The Clebsch surface is the surface given by the
above equation.
It is, up to homography, the only cubic surface for which
the group of homography under the action of which it is invariant is the
group S5 of
permutations of five objects (cf. the invariance under the 120 permutations
of the coordinates
).
It has the distinctive feature that its 27 lines (that
all smooth cubic surfaces have) are all real.
These 27 lines are divided into two groups:
The Clebsch surface is, up to homography, the only cubic
surface to have 10 triple Eckardt points.
| 2) The 12 lines of the principal double
six
In the complex space, these lines have a very simple definition: they are the lines joining the point with homogeneous coordinates |
 |
It can be proved that these twelve lines form the so-called principal "double six"
Here are various affine representations of this surface:
|
The change of coordinates Homogeneous equation: This representation has the inconvenient that the plane |
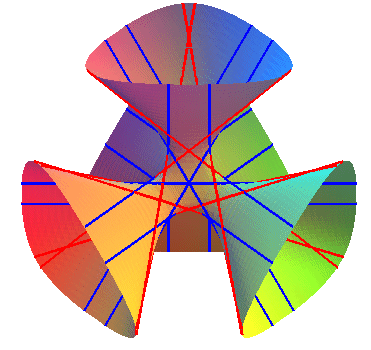
here, the diagonals in blue, and the double six in red. |
Affine representation chosen by Clebsch and Klein in 1872
for the model created by the sculptor Adolf Weiler:
| The change of coordinates defined by gives for k = 4, l= 3 (chosen for aesthetic reasons) the Homogeneous equation: Associated affine Cartesian equation: |
Here are representations using this equation: notice the parallel lines intersecting at an Eckardt point at infinity.
Here is a rational transform such that the first 4 Sylvester
planes form a regular tetrahedron:
| The change of coordinates defined by Homogeneous equation: Associated affine Cartesian equation: i.e. The first 4 Sylvester planes form the regular tetrahedron with vertices the Eckardt points |

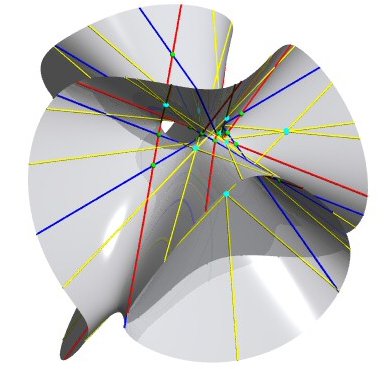
here, the diagonals in blue, and the double six in red. |
Here is a series of views of a representation for which the 10 Eckardt points are at finite distance:
 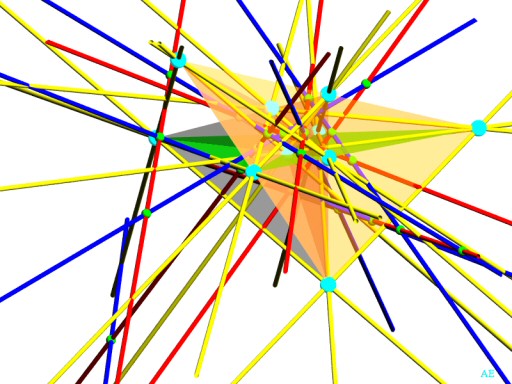 |
See also the Cayley surface.
 |
Engraving by Patrice Jeener, with his kind authorization. |
| WEBOGRAPHY
Alain Esculier's page on the topic: aesculier.fr/fichiersMaple/calculsClebsch/calculsClebsch.html. Another website, by the same: enriques.mathematik.uni-mainz.de/csh/playing/galery/famous.html B. Hunt, The Geometry of Some special Arithmetic Quotients, Lecture Notes in Mathematics, vol.1637, Springer-Verlag 1996. A simple and clear text in German: mathedidaktik.uni-koeln.de/fileadmin/MathematikFiles/kaenders/kaenders_06.pdf |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Alain ESCULIER 2017