Dupin indicatrix

DUPIN INDICATRIX

Charles Dupin (1784-1873): French economist, mathematician and politician.

When a plane parallel to the tangent plane at a point M of a surface tends to this plane, its section with the surface tends to become the homothetic image of a curve which, after proper normalization, is the Dupin indicatrix of the point of the surface.
When the point is not a planar point, the Dupin indicatrix is the union of two conics, with equation in the tangent plane with the frame of the principal directions, where R₁ and R₂ are the principal radii of curvature of the surface at M. These principal directions are given by the two curvature lines passing by the point.

When R₁ and R₂ are finite and have the same sign, the indicatrix is an ellipse, and the point is said to be elliptic (and called umbilic when R₁ = R₂).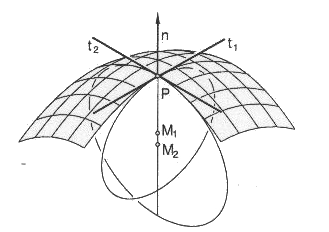

When R₁ et R₂ are finite and have opposite signs, the indicatrix is the union of two conjugate hyperbolas, and the point is said to be hyperbolic; the two asymptotes of these hyperbolas are the asymptotic tangents at M, tangent to the two asymptotic lines passing by M.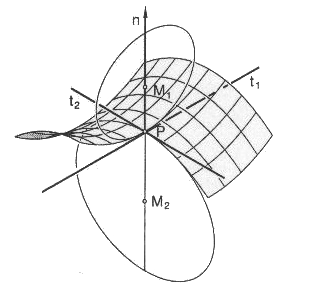

When R₁ or R₂ is infinite, the indicatrix is the union of two parallel lines, and the point is said to be parabolic or torsal.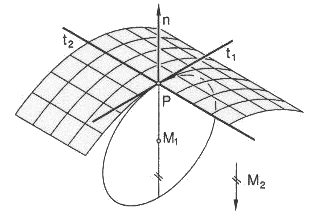

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra

When R₁ and R₂ are finite and have the same sign, the indicatrix is an ellipse, and the point is said to be elliptic (and called umbilic when R₁ = R₂).
When R₁ et R₂ are finite and have opposite signs, the indicatrix is the union of two conjugate hyperbolas, and the point is said to be hyperbolic; the two asymptotes of these hyperbolas are the asymptotic tangents at M, tangent to the two asymptotic lines passing by M.
When R₁ or R₂ is infinite, the indicatrix is the union of two parallel lines, and the point is said to be parabolic or torsal.