Two-sheeted hyperboloid

TWO-SHEETED HYPERBOLOID H₂

Cartesian equation:

.
For a = b: two-sheeted hyperboloid of revolution.
For a = b = c: rectangular two-sheeted hyperboloid.

Small exercise: of what type is the quadric

?
Answer: by a change of orthonormal frame such that OZ is the line x=y=z we get

hence H1 for

, a cone for

, H2 for

, all of them of revolution around OZ.

Cartesian parametrization
- the coordinate lines of which give a family of hyperbolas and a family of ellipses: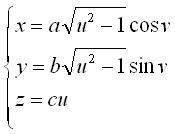

, or

, or also:

.
- the coordinate lines of which are the curvature lines:

with, for c < b < a: .
The values u = v = a² give the 4 umbilics, with coordinates .
Total curvature: where is the distance from O to the tangent plane at the considered point.
Case of the rectangular hyperboloid .
Cylindrical equation : .
First fundamental quadratic form : .
Gauss curvature : .

The two-sheeted hyperboloid is the only non-connected quadric.

The two-sheeted hyperboloid of revolution can be defined as the surface of revolution generated by the rotation of a hyperbola around its transverse axis. It is the locus of the points M satisfying , where F and F' are the common foci of these hyperbolas.

View of the curvature lines of the two-sheeted hyperboloid; they are circles and hyperboloids only in the case of the hyperboloid of revolution, otherwise, they are biquadratics.
The 4 singularities are the umbilics.

View of one of the two families of circles included in any H2, even if it is not of revolution, with the two corresponding umbilics.