SPIRALE DE POINSOT
Poinsot
spiral, Poinsotsche Spirale

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SPIRALE DE POINSOT
Poinsot
spiral, Poinsotsche Spirale


| Courbe déterminée par Cotes
en 1722, puis obtenue comme cas
particulier d'herpolhodie par Poinsot en 1851.
Louis Poinsot (1777 - 1859) : mathématicien français. Autre nom, comprenant aussi les épis : spirale de Cotes. |
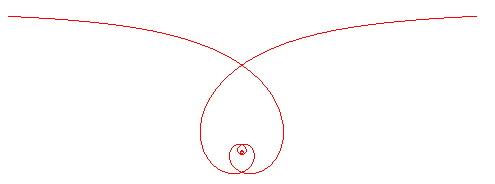
La spirale de Poinsot
est la courbe d'équation polaire ci dessous.
| Équation polaire : |
Lorsque
-
on obtient une spirale logarithmique
-
on obtient une spirale bornée semblable à
.
-
: une spirale à asymptote semblable à
.
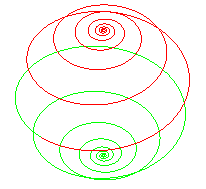
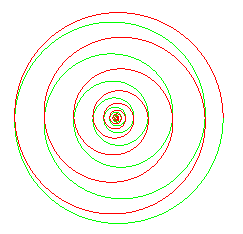
| La spirale de Poinsot bornée est la projection
orthogonale sur le plan de l'équateur de la loxodromie
de la sphère : |
  |
|
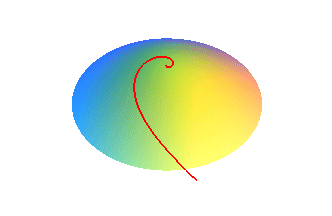
La spirale de Poinsot à asymptote est la projection de la courbe tracée sur un hyperboloïde à deux nappes : |
 |
Les spirales de Poinsot sont solutions du problème
consistant à déterminer les trajectoires dans le vide d'un
point matériel soumis à une force centrée sur O
proportionnelle à
(cette force est d'après la formule de Binet proportionnelle à
qui vaut ici
,
avec
)
; les autres solutions sont les épis
avec comme cas intermédiaire la spirale
hyperbolique, voir ce
lien.
Les spirales de Poinsot sont les inverses des spirales
de la tige en rotation.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022