Si M0 est le point courant de , le point courant M de la podaire est défini par  ce qui donne : en cartésien,  en complexes, et  en polaire, avec  ; on a alors  (voir les notations). Si l'équation tangentielle de  est f(u, v, w) = 0 (ce qui signifie que f(u, v, w) = 0 est une condition pour que la droite  soit tangente à ), l'équation polaire de la podaire par rapport à O est  et son équation cartésienne est . Si l'équation podaire de la courbe  est : , celle de sa podaire est : .

La (courbe) podaire d'une courbe  par rapport à un point O (ou de pôle O) est le lieu des pieds des perpendiculaires issues de O aux tangentes à la courbe .
 
 

C'est donc aussi l'enveloppe des cercles de diamètre [OM0], M0 décrivant  (propriété donnant une construction de la normale donc de la tangente à la podaire).

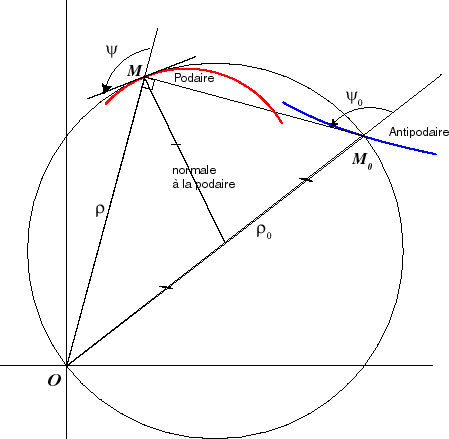
Démontrez que  !

C'est enfin l’inverse par rapport à tout cercle de centre O de la polaire de  par rapport à ce cercle.
La podaire est homothétique de l'orthotomique.

La courbe dont une courbe est la podaire s'appelle l'antipodaire.

Exemples :

- Il y a identité entre les podaires de parabole par rapport à un point autre que le foyer, les courbes cissoïdales d’un cercle et d’une droite relativement à un point du cercle, et les cubiques circulaires rationnelles ; plus précisément : la podaire par rapport à O de la parabole de foyer F et de tangente au sommet (T) est la courbe cissoïdale de pôle O du cercle de diamètre [OF] et de la droite (D) image de (T) par la translation de vecteur .

- Il y a identité entre les podaires de conique à centre, les courbes cissoïdales de deux cercles relativement à un point d’un des cercles, et les quartiques bicirculaires rationnelles.
 

Autres exemples regroupés en tableau :
 

antipodaire (ou orthocaustique)	pôle (position par rapport à l'antipodaire)	pôle (position par rapport à la podaire)	podaire
droite	quelconque	quelconque	point (projeté du pôle sur la droite)
parabole	foyer	extérieur à la droite	droite (tangente au sommet de la parabole)
"	autre que le foyer	point singulier	cubique circulaire rationnelle
"	à l'intérieur de la parabole	point isolé	cubique circulaire rationnelle acnodale
"	sur la partie interne de l'axe de la parabole		cubique de Sluze
"	au milieu du segment [SF]	point isolé	visiera
"	sur la parabole	point de rebroussement	cissoïde
"	au sommet	point de rebroussement	cissoïde droite
"	à l'extérieur de la parabole	point double	cubique circulaire rationnelle crunodale
"	sur la tangente au sommet	point double	ophiuride
"	sur la directrice	point double	strophoïde
"	pied de la directrice	point double	strophoïde droite
"	symétrique du foyer par rapport à la directrice	point double	trisectrice de Maclaurin
conique à centre	foyer	extérieur au cercle	cercle (principal de la conique)
"	différent du foyer	point singulier réel	quartique  bicirculaire rationnelle s'obtenant par antiparallélogramme articulé
"	centre	point singulier réel	courbe de Booth
cercle	extérieur au cercle	point double	limaçon de Pascal à boucle
"	sur le cercle	point de rebroussement	cardioïde
"	intérieur au cercle	point isolé	limaçon de Pascal sans boucle
"	centre	centre	même cercle
hyperbole équilatère	centre	point double	lemniscate de Bernoulli
cubique de Tschirnhausen	foyer (au 8/9 ème du segment [point double, sommet])	foyer	parabole
cissoïde de Dioclès	point de coordonnées (4a, 0)	sommet	cardioïde
cardioïde	point de rebroussement	sommet de la boucle	sextique de Cayley
cardioïde	centre du cercle conchoïdal	sommet de la boucle	limaçon trisecteur
cardioïde	point de coordonnées (-a,0)	point triple	néphroïde de Freeth
deltoïde	quelconque		folium
deltoïde	à l'intérieur de la deltoïde		trifolium
deltoïde	sur un axe de symétrie de la deltoïde		folium droit
deltoïde	sur la deltoïde		bifolium
deltoïde	centre		trifolium régulier
deltoïde	point de rebroussement		folium simple
deltoïde	sommet		bifolium régulier
cycloïde à centre	centre	centre	rosace
astroïde	quelconque		scarabée
astroïde	centre	centre	rosace à quatre branches
paracycloïde	centre du repère	pôle	spirale
hypercycloïde	centre du repère	pôle	spirale
spirale sinusoïdale de paramètre n = –1/m	centre	centre	spirale sinusoïdale  de paramètre n/(n+1) = –1/(m–1)
spirale logarithmique	centre	centre	spirale logarithmique
développante de cercle	centre	centre	spirale d'Archimède
spirale hyperbolique	centre	centre	spirale tractrice
spirale de Norwich	centre	centre	spirale de Galilée
croix de malte	centre	centre	oeuf double
courbe de Talbot	centre	centre	ellipse
développée de conique à centre	foyer		courbe de Jerabek

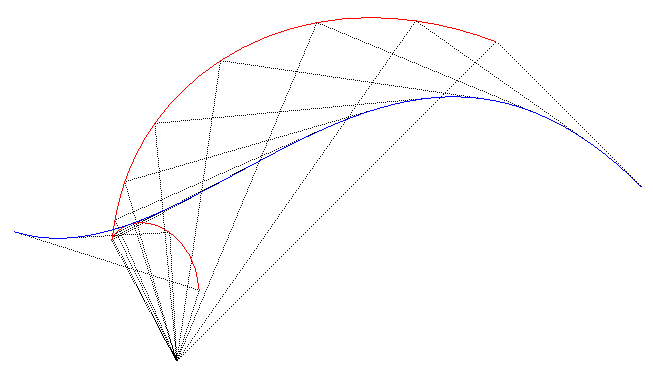
Citons le beau théorème de Steiner-Habich : Si une courbe (C) roule sur une droite (D), et si (R) est la roulette décrite par un point M du plan de cette courbe, alors on peut faire rouler un exemplaire de la podaire (P) de (C) par rapport à M sur (R), de sorte que le point M décrive la droite (D). Le couple ((R), (P)) est alors un couple roue-route. Voir de très nombreux exemples sur ce dernier lien.

Ainsi que cet autre théorème de Steiner (1825) : Le lieu des points par rapport auxquels la podaire d'une courbe fermée possède une aire algébrique donnée sont situés sur un cercle centré au "barycentre de courbure" de la courbe ; ce barycentre est calculé en attribuant aux points de la courbe un poids égal à la courbure en ce point.

Notons qu'on définit le polygone podaire par rapport à O d'un polygone donné comme le polygone dont les sommets successifs sont les projetés successifs de O sur les côtés (prolongés) successifs du polygone de départ. Cette notion discrète concorde avec la notion continue lorsqu'on fait "tendre" le polygone vers une courbe.

On définit aussi la contre-podaire de  par rapport à O comme le lieu des pieds des perpendiculaires issues de O aux normales à . La contre-podaire n'est alors autre que la podaire de la développée.

Voir aussi les surfaces podaires.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020