BASE, ROULANTE ET ROULETTES
D'UN MOUVEMENT PLAN SUR PLAN
Base curve
(or fixed centrode), rolling curve (or moving centrode) and roulettes
in a rigid
motion of a moving plane over a fixed plane
Fixkurve (od. Rastpolbahn), rollende Kurve (od Gangpolbahn)
und Rollkurven in einem Bewegungablauf zweier Ebenen
| Le mouvement plan sur plan a été étudié
en généralité par W.H.
Besant en 1869, avec pour précurseurs pour des cas particuliers
: Dürer en 1525, D. Bernoulli, La Hire, Desargues, Leibniz, Newton,
Maxwell etc. |
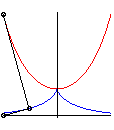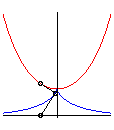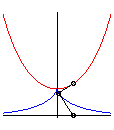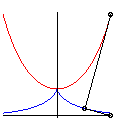
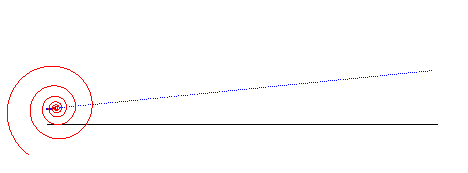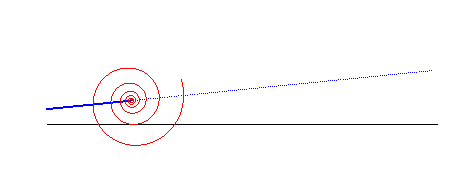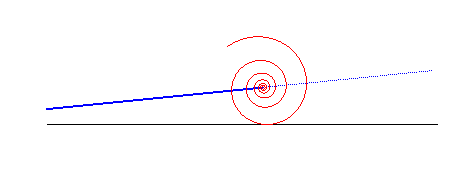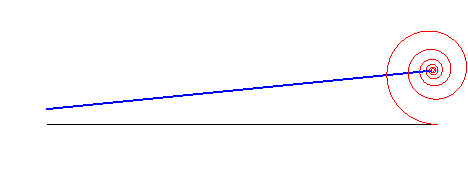
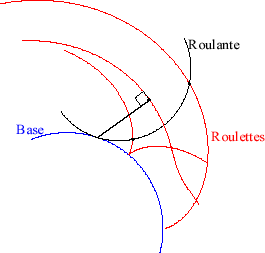
| La base d'un mouvement plan sur plan est la courbe
engendrée par les positions successives dans le plan fixe
du centre instantané de rotation du mouvement du plan mobile.
La roulante est la courbe engendrée par
ces positions successives, dans le plan mobile.
Durant le mouvement, la roulante roule sans glisser sur
la base, qui est son enveloppe.
Les roulettes (ou trajectoires) sont les
courbes tracées sur le plan fixe par les points du plan mobile.
La droite joignant le point de contact entre la base
et la roulante au point traceur est normale à la roulette (théorème
de Descartes).
Voir des exemples d'étude de mouvement plan sur
plan sur cette page, ainsi que la notion
de glissette, qui permet de
définir divers mouvements plan sur plan.
Lorsque le mouvement du plan mobile est un mouvement
de translation, la base et la roulante sont rejetées à l'infini
(voir à reptoire). |
 |
 |
Le plan est rapporté au repère fixe : 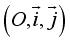 et au repère mobile dépendant du temps t :
et au repère mobile dépendant du temps t :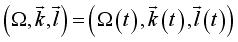 ; le point
; le point 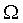 a pour affixe :
a pour affixe : 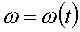 et le vecteur
et le vecteur 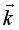 :
: 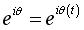 dans
le repère fixe. dans
le repère fixe.
Un point M = M(t) a une affixe :
m =
m(t) dans le repère fixe et une affixe : 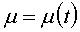 dans le repère mobile reliés par la relation :
dans le repère mobile reliés par la relation : 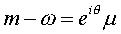 ,
d'où en dérivant par rapport au temps : ,
d'où en dérivant par rapport au temps : 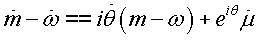 (1) .
(1) .
Soit N(t, u), d'affixe n(t,
u), le point qui a dans le repère mobile à l'instant
t
la position qu'avait (ou qu'aura) le point M à l'instant
u
; on a : 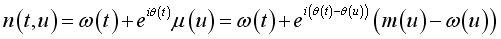 . . |
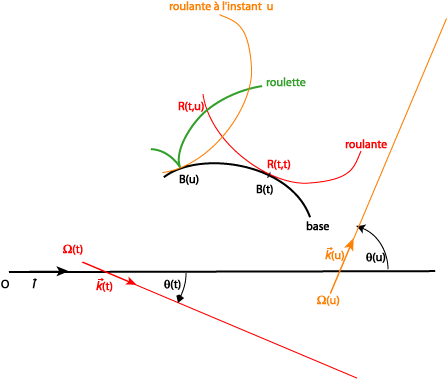
A l'instant t, le centre instantané de
rotation 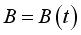 du repère mobile par rapport au plan fixe (centre qui est le point
courant de la base), est le point fixe dans le plan mobile qui a
une vitesse nulle par rapport au repère fixe ; il est donc défini
par
du repère mobile par rapport au plan fixe (centre qui est le point
courant de la base), est le point fixe dans le plan mobile qui a
une vitesse nulle par rapport au repère fixe ; il est donc défini
par 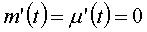 ,
ce qui donne par (1) ,
ce qui donne par (1) 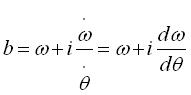 ,
soit ,
soit 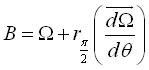 ; l'affixe
; l'affixe 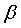 de B dans le repère mobile est définie par
de B dans le repère mobile est définie par 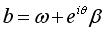 ,
soit ,
soit 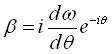 . .
On montre que l'on a alors 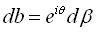 ,
ce qui exprime que la roulante roule sans glisser sur la base. ,
ce qui exprime que la roulante roule sans glisser sur la base.
La roulante est, à chaque instant t,
la courbe décrite par les point d'affixe 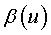 dans le repère mobile, pour u décrivant
dans le repère mobile, pour u décrivant 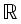 ; son point courant
; son point courant 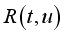 (R est à
B ce que N est à M ci-dessus)
a pour affixe dans le repère fixe :
(R est à
B ce que N est à M ci-dessus)
a pour affixe dans le repère fixe : 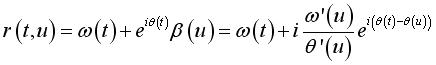 . .
Une roulette est la trajectoire d'un point M
fixe dans le repère mobile ; elle est définie par 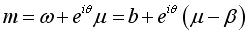 (
(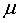 est ici constant). est ici constant).
Exemple de calcul de roulette connaissant la base et
la roulante, pour la cycloïde
:
données 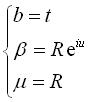 ;
; 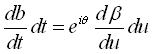 s'écrit
: s'écrit
: 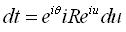 , d'où , d'où 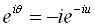 ,
et ,
et 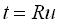 , donc
: , donc
:
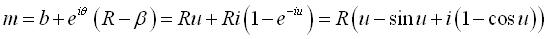 . . |
Voici, dans le cas où le vecteur 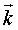 est colinéaire à
est colinéaire à 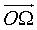 ,
le calcul de la base, de la roulante et des roulettes connaissant le mouvement
plan sur plan, défini par la donnée de la trajectoire du
point W (équation polaire ,
le calcul de la base, de la roulante et des roulettes connaissant le mouvement
plan sur plan, défini par la donnée de la trajectoire du
point W (équation polaire 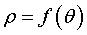 )
. )
.
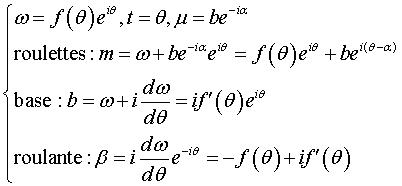 La base a donc pour équation polaire
La base a donc pour équation polaire 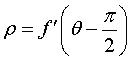
et la roulante pour paramétrisation cartésienne
: 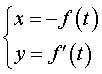 . . |
Exemples :
- Lorsque le plan mobile est le plan
lié à la tangente à une courbe (le point de tangence
étant fixe sur la droite), la base est la
développée
de cette courbe, et la roulante, la normale. La courbe est alors l'une
des roulettes (voir le cas dual du cas n°1 dans la page
sur les glissettes).
- Lorsque la roulante est la symétrique
de la base par rapport à une tangente, la roulette est la courbe
orthotomique
de la base par rapport au symétrique du point traceur par rapport
à la tangente (point qui est fixe) ; par exemple :
- les roulettes
du centre d'une ellipse roulant sur une ellipse symétrique sont
les ovales de Booth
- les roulettes
du centre d'une hyperbole roulant sur une hyperbole symétrique sont
les lemniscates de Booth
- la roulette
du sommet d'une parabole roulant sur une parabole symétrique est
la cissoïde de Dioclès
Les exemples exhaustifs se trouvent à podaire.
- Les exemples où la base
est rectiligne ont été mis sur une page
spécifique.
- Lorsque la roulante est rectiligne,
et le point traceur sur la droite, la roulette est une développante
de la base.
- Lorsqu'une roulette est rectiligne,
la base et la roulante forment un couple
route-roue, tandis que lorsqu'une roulette est circulaire, la
base et la roulante ont des
profils
conjugués.
Autres exemples :
Remarque : même lorsque base et roulante sont algébriques,
la roulette peut être transcendante (cf. la cycloïde).
On désigne aussi plus généralement
par roulette d'une courbe fixe du plan mobile l'enveloppe de cette
courbe dans le plan fixe. Les centres de courbure des deux courbes sont
alors reliés par le théorème
d'Euler-Savary.
Exemples :
- la base est l'enveloppe de la roulante
(qui est la seule courbe qui ne glisse pas sur sa roulette).
- la directrice d'une parabole roulant
sur une droite enveloppe la chaînette
tracée par son foyer.
- un diamètre d'un cercle roulant
sans glisser sur une droite enveloppe une cycloïde,
et toute droite du plan mobile enveloppe une développante de cycloïde.
- un diamètre d'un cercle roulant
sans glisser à l'intérieur d'un cercle de rayon double enveloppe
une astroïde, et la droite
perpendiculaire à ce diamètre en une extrémité
enveloppe une croix de Malte
; plus généralement avec des cercles de rayons quelconques,
on obtient comme enveloppes du diamètre du cercle roulant les cycloïdes
à centre et comme enveloppes d'une droite quelconque les développantes
de cycloïdes à centre.
- l'antipodaire
d'une courbe est la roulette de la perpendiculaire en M à
(OM), M décrivant la courbe, et le plan mobile étant
le plan dans lequel M et (OM) sont fixes.
Le mouvement d'une sphère sur une sphère
isométrique conduit à des notions de base, roulante et roulettes
tout à fait similaires à celles du mouvement plan sur plan.
Voir par exemple, les trochoïdes
sphériques du deuxième type.
© Robert FERRÉOL
2010