Notion étudiée par Besant en 1869.

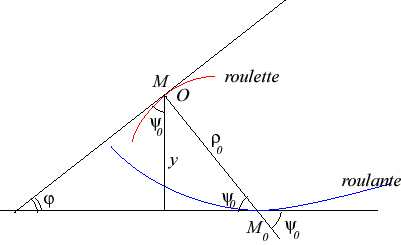
Etant donné une courbe () et un point O lié à (), la roulette à base rectiligne associée est la trace du point O lorsque la courbe () roule sans glisser sur une droite fixe. Il s'agit donc d'un mouvement plan sur plan dont la base est rectiligne.
 
 

Les formules reliant les équations de la roulante () et de la roulette () sont . Partant d'une roulante , on obtient la roulette . Partant inversement d'une roulette , on obtient la roulante , dont la podaire s'obtient plus simplement en polaires par les formules : . L'abscisse curviligne et le rayon de courbure de la roulante sont donnés par :  En complexes, la relation s'écrit :  .

Exemples :

figure	roulante	point traceur	roulette
	cercle	sur le cercle	cycloïde
	cercle	hors du cercle	trochoïde
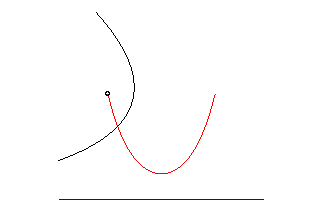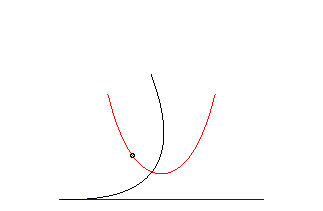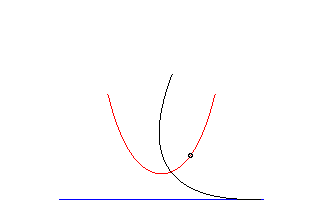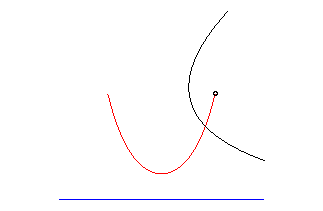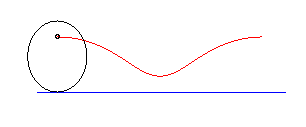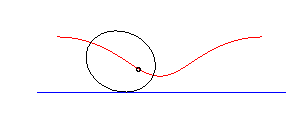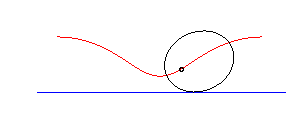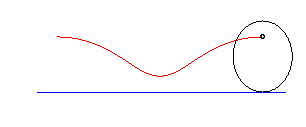
	parabole	foyer de la parabole	chaînette
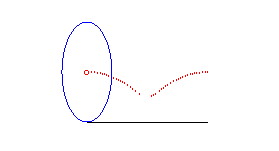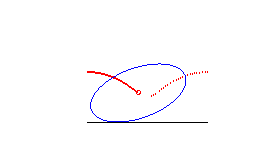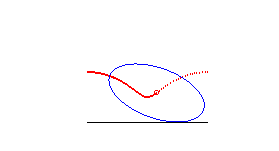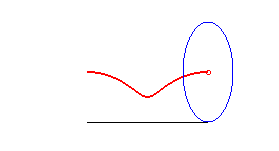
	conique à centre	foyer de la conique	roulette de Delaunay
	conique à centre	centre de la conique	roulette de Sturm
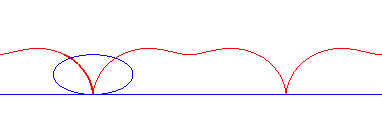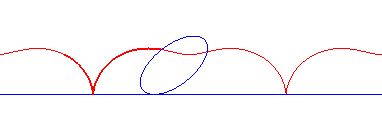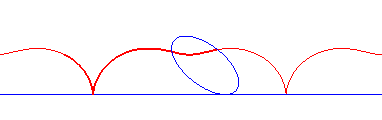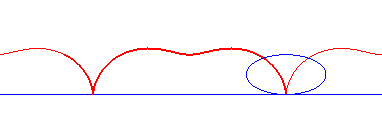	ellipse	quelconque	roulette à base rectiligne d'ellipse
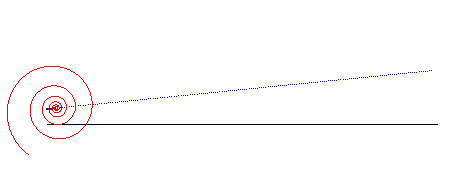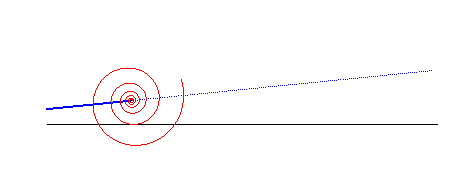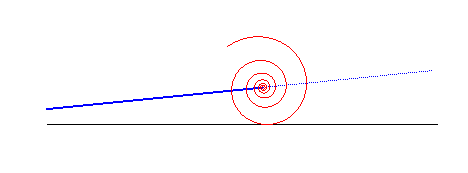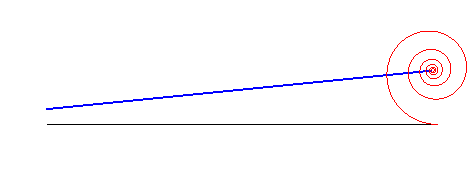	spirale logarithmique	centre de la spirale	droite
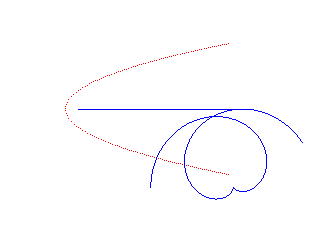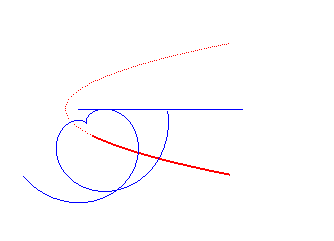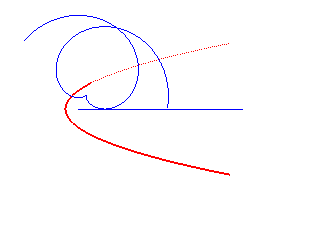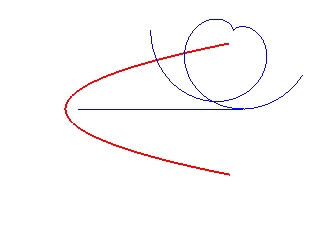	développante de cercle	centre du cercle	parabole dont la base est l'axe de symétrie
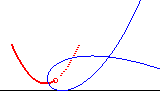	cubique de Tschirnhausen	foyer de la cubique	parabole dont la directrice est la droite de roulement
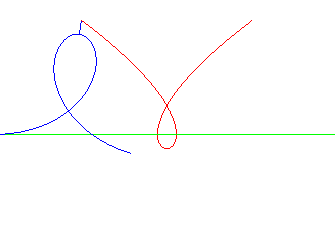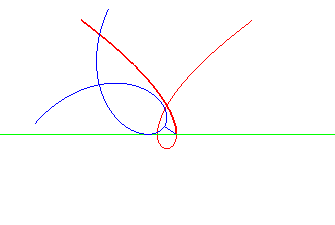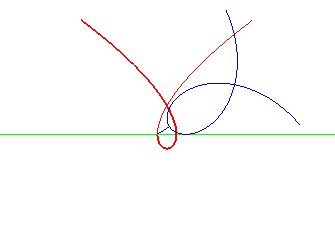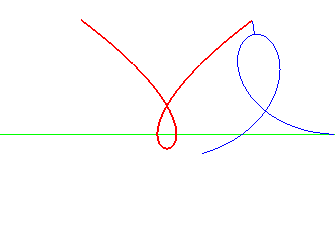	Spirale de Norwich	Pôle de la spirale	cubique de Tschirnhausen
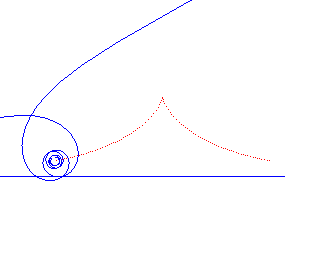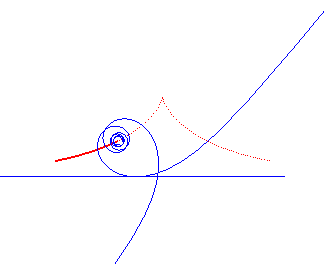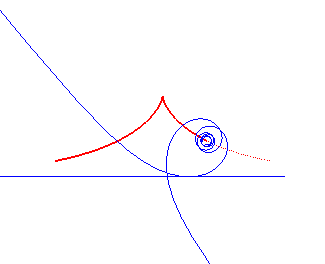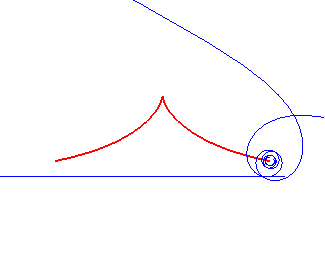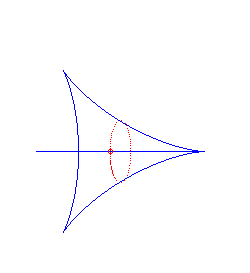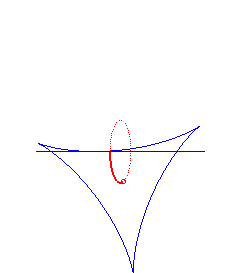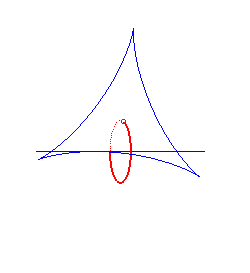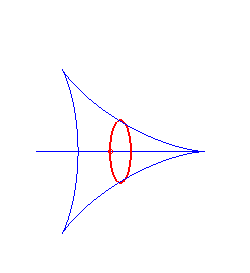
	spirale hyperbolique	centre de la spirale	tractrice
	cycloïde à centre	centre de la cycloïde	ellipse
	spirale sinusoïdale d'indice n	pôle de la spirale	courbe de Ribaucour d'indice 1+1/n

Les roulettes à base rectiligne d'une courbe étant identiques aux glissettes à base rectiligne de toute développante de cette courbe, voir aussi d'autres exemples à glissette.

Comparer avec la notion de couple roue-route, où cette fois c'est la roulette qui est rectiligne au lieu de la base.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2017