Courbe de Rosillo

COURBE DE ROSILLO
Rosillo curve, Rosillosche Kurve

Courbe étudiée par Nicolas Rosillo en 2009.

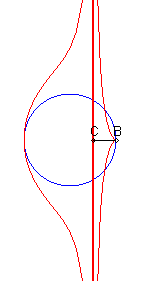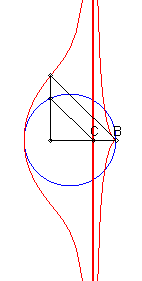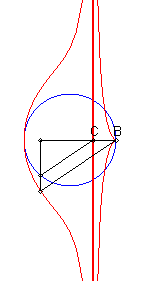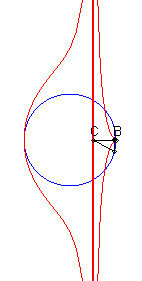
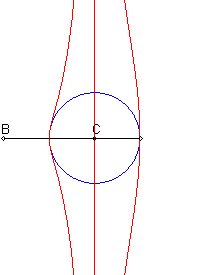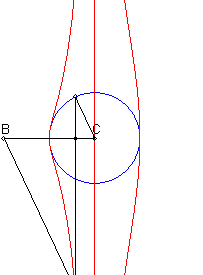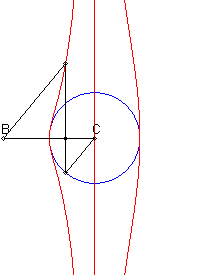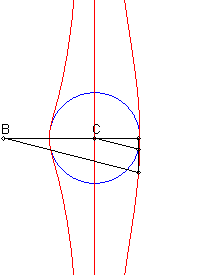
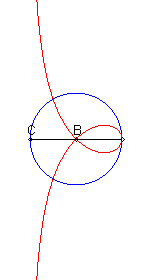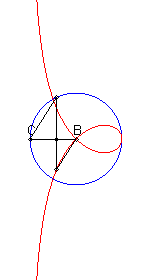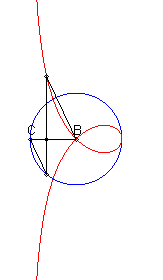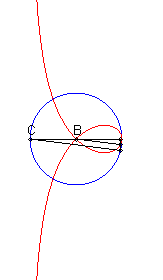
Etant donnés un cercle (C) et deux points B et C d'un de ses diamètres (D), la courbe de Rosillo associée est le lieu des points M tels que si P est l'un des points d'intersection de la perpendiculaire à (D) passant par M avec (C), les droites (BM) et (CP) sont parallèles.

Si (C) est de centre O et de rayon a, B(b,0) et C(c,0) :
Paramétrisation cartésienne : .
Equation cartésienne : ou .
Quartique rationnelle.

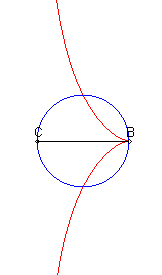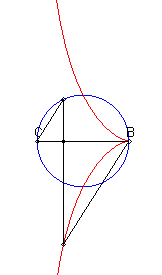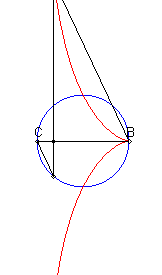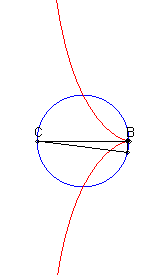
Lorsque C est intérieur au cercle, on obtient une courbe à asymptote (x = c), avec point de rebroussement en B si B est sur le cercle.

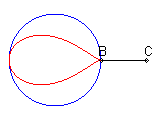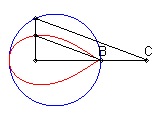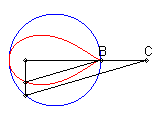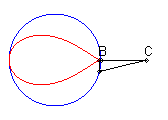
Lorsque C est extérieur au cercle, on obtient une courbe fermée, avec point de rebroussement en B si B est sur le cercle.
On remarquera la forme de coeur, de huit disymétrique, de larme ou d'oeuf.

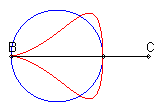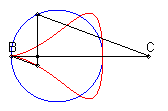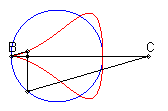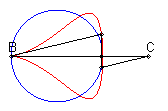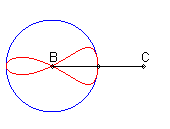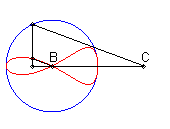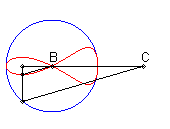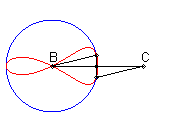
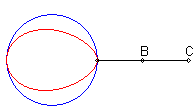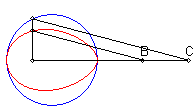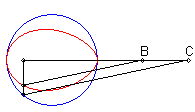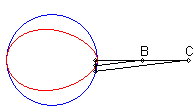Lorsque C est au centre du cercle (c = 0), on obtient les conchoïdes de droite (pôle = B, droite = perpendiculaire à (D) passant par C, module = rayon du cercle)

Lorsque C est sur le cercle, la courbe se décompose en une droite et une cubique, d'équation ; on obtient ainsi toutes les hyperboles cubiques du type avec P de degré 3 ayant une racine réelle double et un coefficient dominant positif.
Si B est diamétralement opposé à C, on obtient la cissoïde droite et si B est au centre, on obtient la strophoïde droite.

Comparer avec les oeufs de Granville et les kiéroïdes.

Quelques vues de surfaces de révolution engendrées par la rotation d'une courbe de Rosillo autour de son axe.

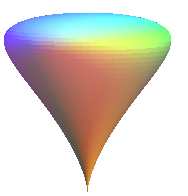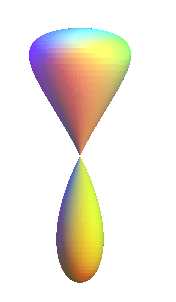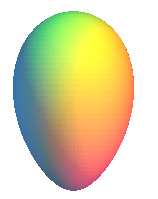courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Lorsque C est intérieur au cercle, on obtient une courbe à asymptote (x = c), avec point de rebroussement en B si B est sur le cercle.
Lorsque C est extérieur au cercle, on obtient une courbe fermée, avec point de rebroussement en B si B est sur le cercle. On remarquera la forme de coeur, de huit disymétrique, de larme ou d'oeuf.
Lorsque C est au centre du cercle (c = 0), on obtient les conchoïdes de droite (pôle = B, droite = perpendiculaire à (D) passant par C, module = rayon du cercle)
Lorsque C est sur le cercle, la courbe se décompose en une droite et une cubique, d'équation ; on obtient ainsi toutes les hyperboles cubiques du type avec P de degré 3 ayant une racine réelle double et un coefficient dominant positif. Si B est diamétralement opposé à C, on obtient la cissoïde droite et si B est au centre, on obtient la strophoïde droite.