Rosillo curve

ROSILLO CURVE

Curve studied by Nicolas Rosillo in 2009.

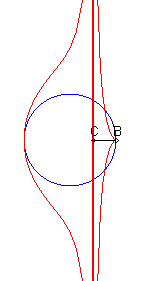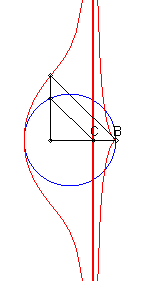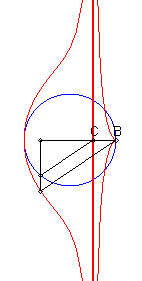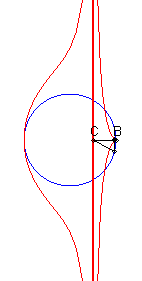
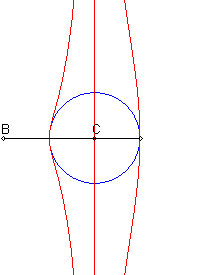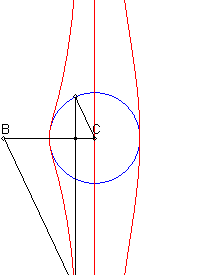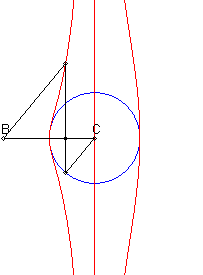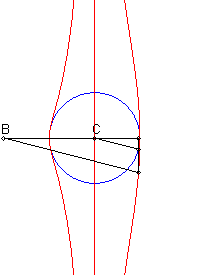
Given a circle (C) and two points B and C on one of its diameters (D), the associated Rosillo curve is the locus of the points M such that if P is one of the intersection points between the line perpendicular to (D) passing by M and (C), the lines (BM) and (CP) are parallel.

If (C) is the circle with centre O and radius a, B(b,0) and C(c,0) :
Cartesian parametrization: .
Cartesian equation: or .
Rational quartic.

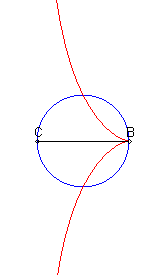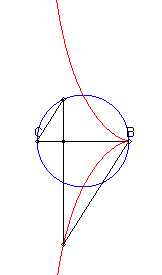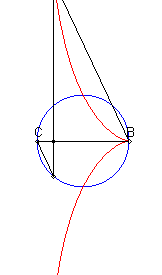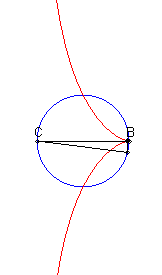
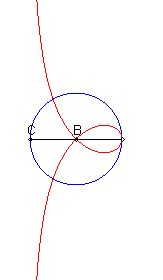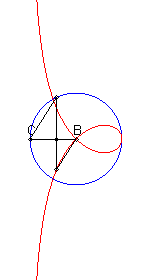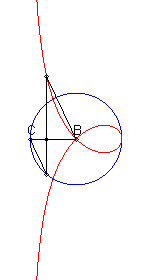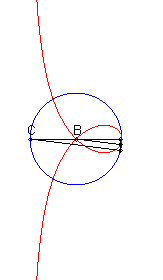
When C is inside the circle, we get a curve with an asymptote (x = c), and a cuspidal point at B if B is on the circle.

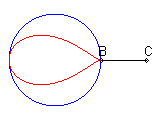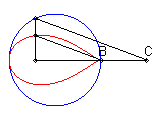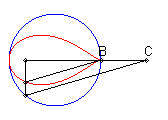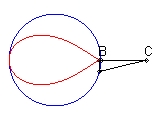
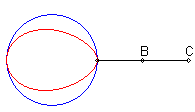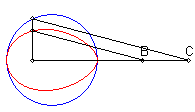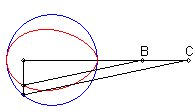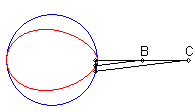
When C is outside the circle, we get a closed curve, with a cuspidal point at B if B is on the circle.
Notice the shape of a heart, a dissymmetrical eight, a tear or of an egg.

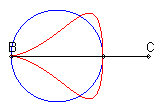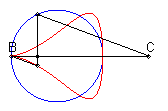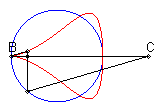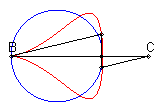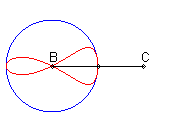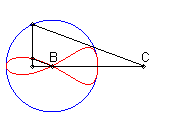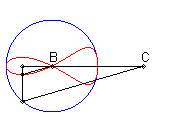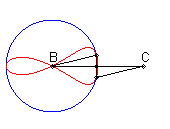
When C is on the centre of the circle (c = 0), we get the conchoids of Nicomedes (pole = B, line = perpendicular to (D) passing by C, modulus = radius of the circle)

When C is on the circle, the curve is composed of a line and a cubic, with equation ; we get all the cubical hyperbolas of the type with P of degree 3 having a double real zero and its leading order coefficient being positive.
If B is diametrically opposed to C, then we get the cissoid of Diocles and if B is on the centre, we get the right strophoid.

Compare to the Granville eggs and the kieroids.

Some view of the surfaces of revolution generated by the rotation of a Rosillo curve around its axis.

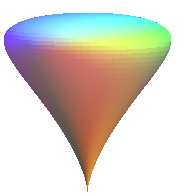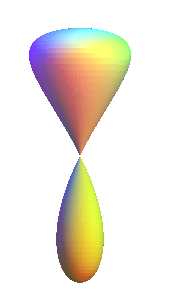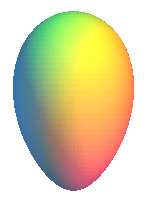next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

When C is inside the circle, we get a curve with an asymptote (x = c), and a cuspidal point at B if B is on the circle.
When C is outside the circle, we get a closed curve, with a cuspidal point at B if B is on the circle. Notice the shape of a heart, a dissymmetrical eight, a tear or of an egg.
When C is on the centre of the circle (c = 0), we get the conchoids of Nicomedes (pole = B, line = perpendicular to (D) passing by C, modulus = radius of the circle)
When C is on the circle, the curve is composed of a line and a cubic, with equation ; we get all the cubical hyperbolas of the type with P of degree 3 having a double real zero and its leading order coefficient being positive. If B is diametrically opposed to C, then we get the cissoid of Diocles and if B is on the centre, we get the right strophoid.