GRANVILLE EGG

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
GRANVILLE EGG

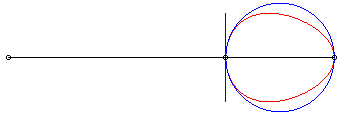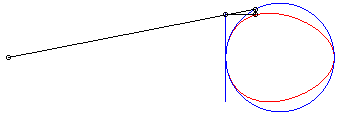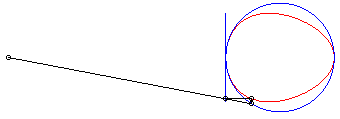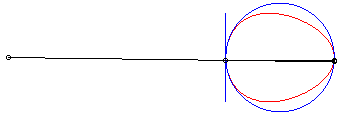
| Curve considered by Granville in 1908. |
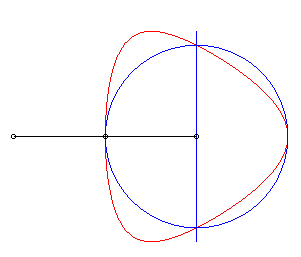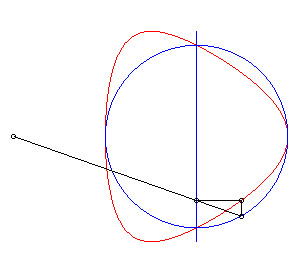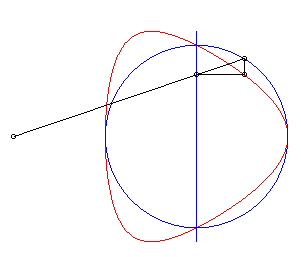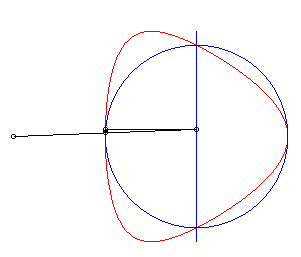
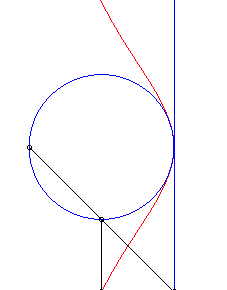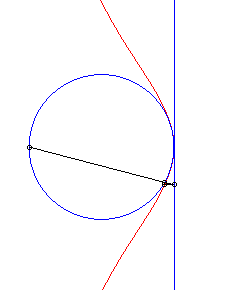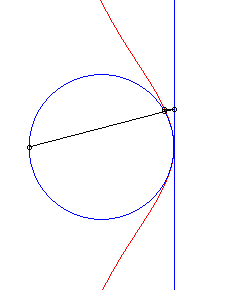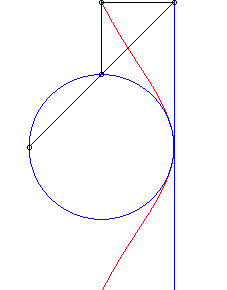
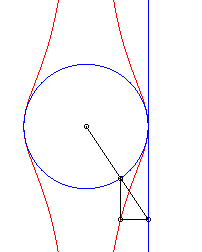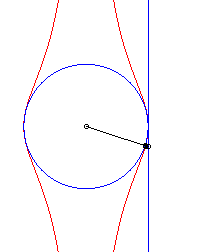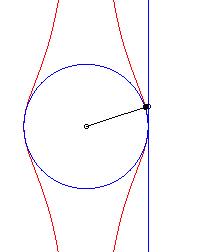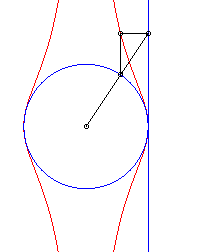
| The Granville egg is the hyperbolism
of a circle with centre B with respect to a point O and a
line (D) perpendicular to (OB)
Parameter for the opposite curve: a = 4, b = 5, r = 1. |
 |
| Cartesian equation for B(b, 0), (D)
: x = a and a circle with radius r: Cartesian parametrization: Rational quartic. |
| Case a = b= 2r | When r = b = a/2, this quartic is composed of the witch of Agnesi and the abscissa axis | When r = a, b = 0, we get the Külp quartic |
 |
 |
 |
Other ovoid quartic: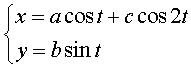 ,
opposite case a = 3, b = 2, c = 1/4 (proposed by Massimo
Vaglieco). ,
opposite case a = 3, b = 2, c = 1/4 (proposed by Massimo
Vaglieco). |
 |
Compare to the Rosillo curves and see other eggs at ovoid.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017