KÜLP QUARTIC
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
KÜLP QUARTIC
| Curve studied by Külp in 1868 (archiv
der Math. und Physik p. 97) and Goormaghtigh
in 1913.
Ludwig Külp (1835 - 1891) : German physiker. Other name: Külp conchoid (because of its resemblance to the conchoid of Nicomedes). |
 |
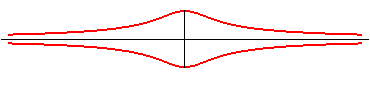Cartesian parametrization:  .
Cartesian equation: 
i.e.  .
Rational quartic. |
The Külp quartic is the hyperbolism of the circle with respect to its centre and a tangent (special case of Granville egg).
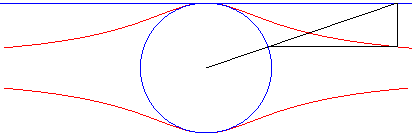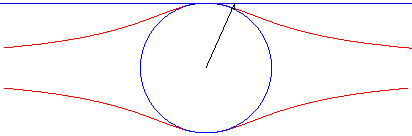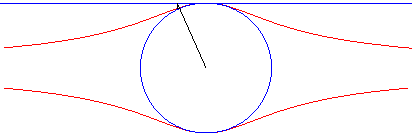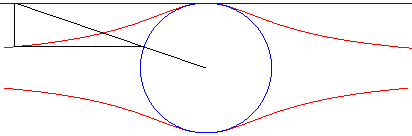
Here, the circle is the circle with diameter [OA] where A(0, a) and the line is y = a.
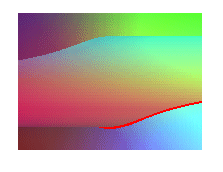
The Külp quartic is also the projection on the plane
xOy
of the biquadratic,
intersection of the cylinder
of revolution
and of the hyperbolic
paraboloid
.
and Cartesian equation 
which is very similar to it:
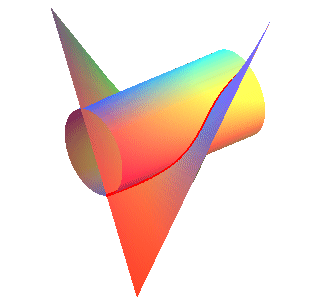
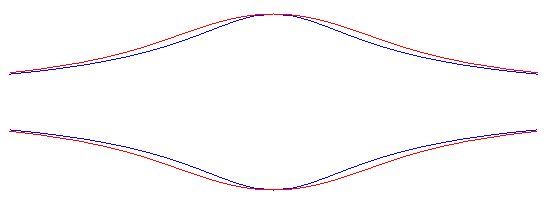
Compare to the witch
of Agnesi.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017