Curve studied by Klein in 1879 (Uber die Transformationen siebenter Ordnung der elliptischen Funktionen, Math. Ann. 14 (1879), 428-471. Œuvres, Tome III, p. 90-136). Félix Klein (1849-1925): German mathematician. Webography: en.wikipedia.org/wiki/Klein_quartic mathworld.wolfram.com/KleinQuartic.html math.univ-lyon1.fr/~germoni/memoires/quartique.pdf

1) The affine Klein quartic:

Cartesian equation:  where  so that pqr = 0 is the reunion of 3 lines forming an equilateral triangle centred on O. Quartic of genus 3. Polar equation: . REMARK 1: the quartic passes by the three intersection points between the circle  and the previous 3 lines and is tangent (doubly) to these 3 lines at these 3 points. REMARK 2: it is a Goursat curve. Compare with the definition of the Kummer surface.

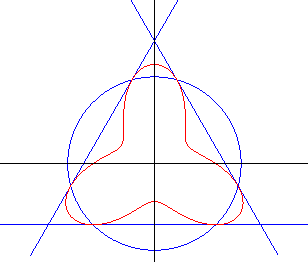
Case , with an illustration of the remark 1.

The same curve, represented along with its Hessian, intersecting the curve at its inflexion points. When , which is the case here, the tangents at the inflexion points are parallel to a symmetry axis.

 
 

The (affine) Klein quartic is the curve above in the special case where . Its particularity is that its tangents at the 6 inflexion points (in green opposite) pass through another inflexion point and form two equilateral triangles. Compare to the Loriga quartic (which has the same property, but is different).

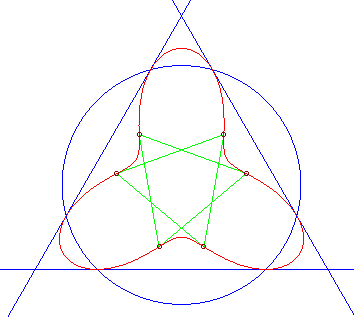2) The projective Klein quartic (projectively equivalent to the previous one):
 

Homogeneous equation:

 

View of the cone (that can be referred to as the "Klein cone") cut by the plane , providing an affine realisation of the projective Klein quartic (different from that of the first paragraph). The cylindrical equation of this cone in a frame where Oz is the axis of rotation is: .

Klein cone, by Alain Esculier

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017