GOURSAT CURVE





| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
GOURSAT CURVE





| Homemade name, given as a tribute to Goursat, who studied
the surfaces with
the symmetries of the regular polyhedra.
Other names: curve with rotation symmetry, curve with radial symmetry. |
The Goursat curves of order n are the curves having the symmetries of a regular polygon with n sides, i.e. for which the group of isometries that leave it invariant is that of this polygon, namely the dihedral group of order 2n.
A curve is therefore a Goursat curve of order n
iff
it is invariant by a rotation of an n-th of a turn (and non-invariant
by a rotation by a smaller angle) and it has an axis of symmetry, or iff
it has exactly n axes of symmetry.
| General polar equation of a Goursat curve of order a multiple of n: | Cartesian equation: |
| hence the general form: (Brocard transformation of the curve |
general form:
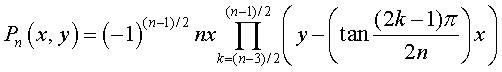 for
odd values of n for
odd values of n |
Examples: the roses:
and their inverses the epispirals, the sinusoidal
spirals:
.
Special cases:
1) n multiple of 2:
| General polar equation: |
General Cartesian equation: in other words: |
Examples with exactly two symmetry axes:
degree 2: ellipses,
hyperbolas
.
degree: the lemniscate of Bernoulli,
the lemniscate of Gerono
,
the bullet nose curve, the
Kampyle
Eudoxus, the Kappa curve, the double
U, the Kulp quartic, the Delanges
trisectrix, the Alain curves, the
devil's
curves.
ETC....
2) n multiple of 3:
| General polar equation: |
General Cartesian equation : Remark: |
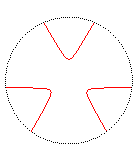
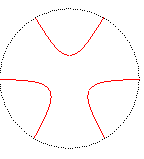
Examples with exactly three symmetry axes:
degree 3: the equilateral
trefoil:
and the Humbert cubic:
(that are the only cubical Goursat 3-curves up to similarity)
 .
.
degree 4: the hypotrochoids
with parameter q = 3:
(including the deltoid, k =
1 and the regular
trifolium, k = 2)
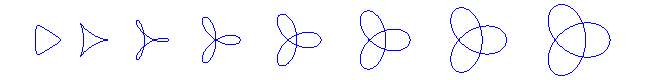 ,
the conchoids of a
regular trifolium
,
the conchoids of a
regular trifolium ,
the Klein quartic
,
the Klein quartic ,
the Loriga quartic.
,
the Loriga quartic.
3) n multiple of 4:
| General polar equation: |
General Cartesian equation: |
Examples with exactly four symmetry axes:
degree 4: the rectangular
crosscurve: ,
the Salmon quartics
.
degree 6: the hypotrochoids
with parameter q = 4: (including the astroid and the quadrifolium),
the conchoids of roses
with parameter 4
with b non-zero
 ,
the windmill,
,
the windmill,
the Loriga sextic
: .
.
4) n multiple of 5:
| General polar equation: |
General Cartesian equation: |
Examples with exactly five symmetry axes:
degree 5: general Cartesian equation: (one
of the 3 numbers k, k', k" being arbitrarily chosen).
(k,k',k")=(1,0,0) gives the epispiral
of order 5 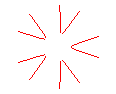 ,
,
gives the curve with 5 double points:
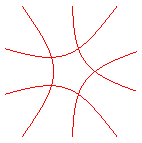
(k,k',k")=(0,-1,0.2) gives 
5) n multiple of 6:
| General polar equation: |
General Cartesian equation: |
Examples with exactly six symmetry axes:
degree 6:  and
and 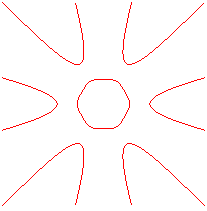
Examples of infinite families:
- the conchoids
of roses:
are Goursat curves of order n (except for even values of n
and b = 0: order 2n)
- all the families of curves defined
symmetrically from n points ,
vertices of a regular polygon (cf. the Curie
principle); in particular, the curves
(
: isophonic
curves,
:
Cayley
equipotential lines,
:
?,
: circles),
the Loriga curves:
,
and the Cassinian curves:
.
| All the curves with polar equation Example opposite: |
 |
| More generally, given a complex function f, with
the same properties, the curve with complex parametrization This case includes the epi- and hypotrochoids ( The more general case 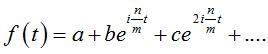 gives the polytrochoids.
gives the polytrochoids.
Opposite, the tritrochoid obtained for |
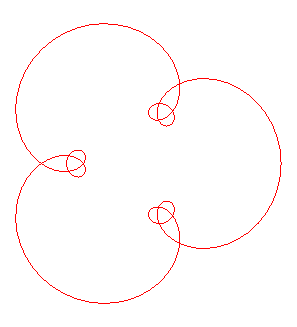 |
| Given f with the same properties, the curve with
complex parametrization This case includes the generalised curves with sinusoidal radius. |
 |
| The curves defined by an intrinsic
equation: Equivalent form: Example opposite: n = 5, m = 3, We get this way all the Goursat curves of order n and nonzero rotation index. |
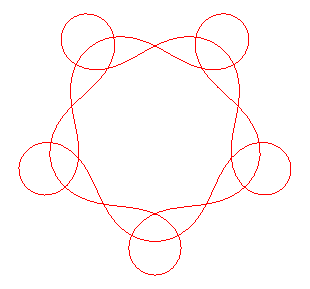 |
Classification of the spherical generic curves, Goursat curves of order n, having exactly n double points.
There are exactly 3 kinds, one of which is composed of
curves with odd order n:
| 2 double points | 3 double points | 4 double points | 5 double points | |
| First kind
Hypotrochoid with parameter q = n, except for n = 2. Rotation index: n -1 |

Lissajous x = cos t , y = sin 3t. |
 |
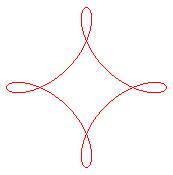 |
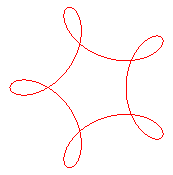 |
| Second kind
Epitrochoid with parameter q = n. Rotation index: n +1 |
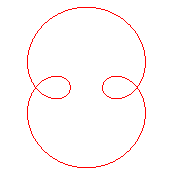 |
 |
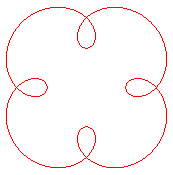 |
 |
| Third kind
Conchoid of a rose with parameter n/2 Rotation index: 2 |
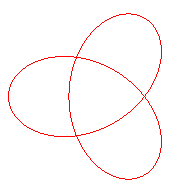 |
 |
See also the Goursat
surfaces,
and the surfaces
with rotation symmetry.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017