ALAIN'S CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ALAIN'S CURVE
| Curve whose study was proposed by Alain Juhel. |
Cartesian equation:  .
Rational quartic. Polar equation:  .
For a > b, polar equation: 
with 
and  .
For 0 < a < b, polar equation: 
with 
and  . |
Alain's curve is the curve defined by the cartesian
equation above.
Here are its different looks:
|
|
|
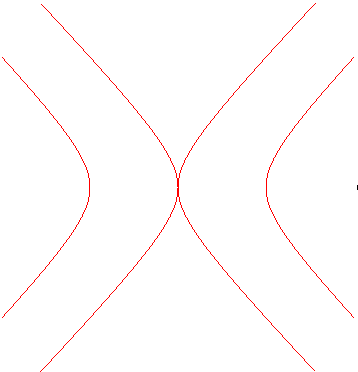
Union of both hyperbolas  . |
 |
|
|
|
Hyperbola 
and its asymptotes. |
 
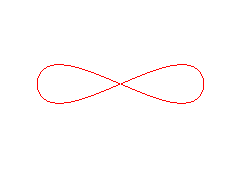
Cylindrical lemniscate |
Alain's curve is the projection onto the plane xOy
of the intersection of the elliptical
cone 
with the hyperbolic
paraboloid  . |
 |
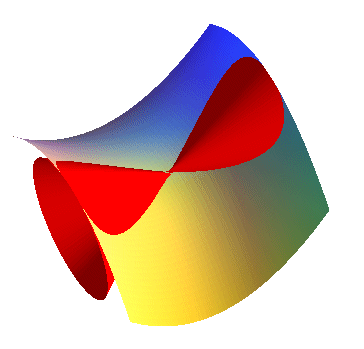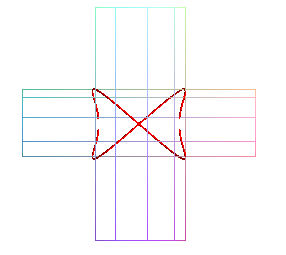
| If a < b, the curve is also the planar projection
of the intersection
of two cylinders of revolution
with common tangent plane, the projection plane being this common plane. More exactly, the projection on the plan xOy of
the cylinders . |
 |
See also Booth's curves,
images of the previous ones by a complex affinity.
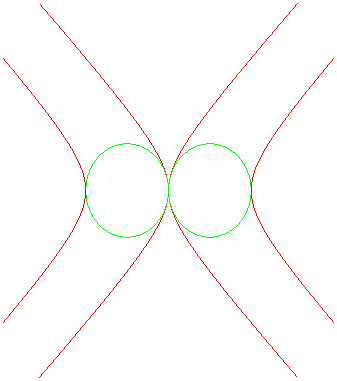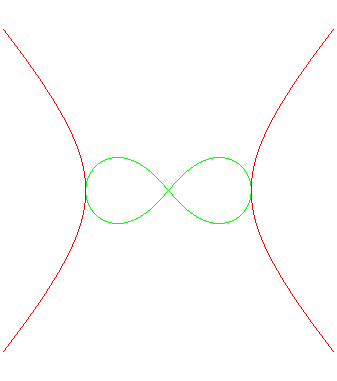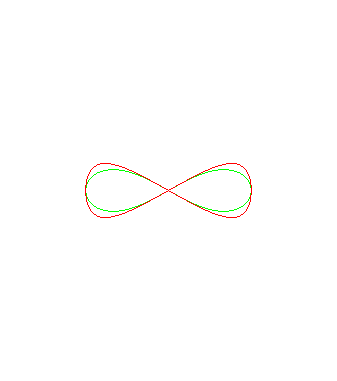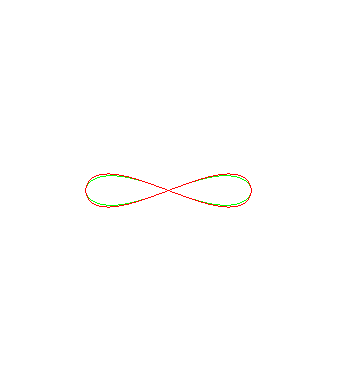
Hereafter, animation of Alain's curves
in red, with the Booth's lemniscates 
in green.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2016
with 
is the curve of equation 
.