Algebraic Curve

ALGEBRAIC CURVE

A curve is said to be algebraic when it's described by a polynomial Cartesian equation with real coefficients; a not algebraic curve is said to be transcendental.

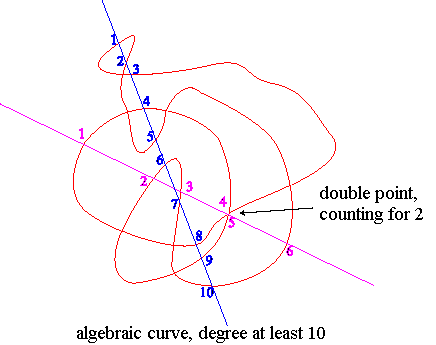
The degree (or sometimes the order) of a flat algebraic curve of equation P(x, y) = 0 is the degree of the polynomial P, supposed square-free. It is also the number of intersection points, counted with their multiplicities, of the curve with any straight line, in the complex projective plan (and the maximum number of intersection points of the curve with a straight line in the real affine plan is a lower bound of the degree and gives very often the degree).

Therefore, a spiral curve, or any curve having an asymptotic point are necessarily transcendental.

The notion of degree is a projective one. In other words, any homography would transform an algebraic curve into an algebraic curve of the same degree.
The curve is said to be decomposable if it is a union of algebraic curves of smaller degree and undecomposable otherwise, in other words, when the polynomial P is irreducible.

Any bounded portion of an algebraic curve can be generated by an articulated mechanism (Kempe's theorem).

The curves of degree 1 are the straight lines, of degree 2 the conics, of degree 3 the cubics, of degree 4 the quartics, of degree 5
quintics, of degree 6 sextics, of degree 7 septics, and of degree 8 biquartics.

Examples of families of algebraic curves of any degrees (for rational values of the parameters): Lissajous curves, Lamé curves, epi- and hypotrochoids, roses, conchoids of roses, folioids, knots curves, epispirals, tear drop curves, cassinian curves, Clairaut's curves, sinusoidal spirals.