COURBE ALGÉBRIQUE 3D
Algebraic
3D curve, algebraïsche 3D Kurve
Une courbe algébrique 3D est l'intersection de
deux surfaces algébriques. Son degré est le produit des degrés
des deux surfaces ; c'est aussi le nombre (compté avec les multiplicités)
de points d'intersection (complexes et projectifs), de la courbe
avec un plan quelconque.
La courbe intersection de deux surfaces algébrique
peut se décomposer en réunion de courbes de degrés
inférieurs dont la somme est égale au degré de la
courbe complète.
Les courbes algébriques 3D de degrés 1 et
2 sont la droite et les coniques.
Les cubiques 3D, de degré 3, sont les intersections
de 2 quadriques réglées ayant une droite commune.
Exemples : la parabole
gauche, líhoroptère.
Les quartiques 3D, de degré 4, sont de deux
espèces :
- première espèce : intersection
de quadriques sans droite commune (appelées les biquadratiques
: 4 = 2 . 2)
- deuxième espèce : intersections
d'une surface cubique avec une quadrique réglée ayant deux
droites communes (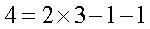 ).
).
Exemple : la ligne de striction d'un hyperboloïde
à une nappe.
Les appellations sont les mêmes que pour les courbes
planes (qui sont des cas particuliers).
Exemple de biquartique : la courbe
d'Archytas.
Exemples de familles de courbes algébriques 3D
de degrés quelconques :
- les courbes 3D de Lissajous
(dont les couronnes sinusoïdales)
- les clélies.
Exemple de section entre deux surfaces algébrique,
montrant que le cadre de tout ceci est la géométrie projective
complexe :
Intersection entre le conoïde
de Plücker (degré 3) : 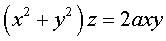 et le cylindre de degré 2 :
et le cylindre de degré 2 : 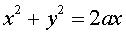 ; en coordonnées homogènes
; en coordonnées homogènes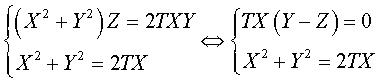 ,
donc l'intersection est formée de l'ellipse
,
donc l'intersection est formée de l'ellipse 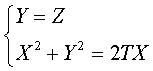 (degré 2), de la droite double
(degré 2), de la droite double 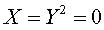 et des deux droites imaginaires
et des deux droites imaginaires 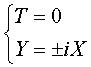 : on a bien 6 = 2 + 2 + 1 + 1.
: on a bien 6 = 2 + 2 + 1 + 1.
© Robert FERRÉOL
2012
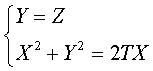 (degré 2), de la droite double
(degré 2), de la droite double